|
|
决定开一个几何题目贴来锻炼几何题...
几何不等式题目:
(i)四边形ABCD中,角CBD < 角ABD, 叫CDB<角 ADB ,
证明 BC+CD< AB+AD |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-4-2006 04:29 PM
|
显示全部楼层
Einstein 曾经说过,不会几何的人,在科学研究领域不会有太大的作为。因为做几何题需要观察力,研究科学也需要观察力!
这里有几个常用的 Identity
ABC 为三角形,边长为 a,b,c 。内切圆(incircle)半径 = r ,外切圆(circumcircle)半径 = R ,面积 = S , 半周长(semiperimeter) = p ,
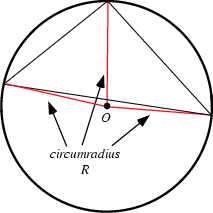
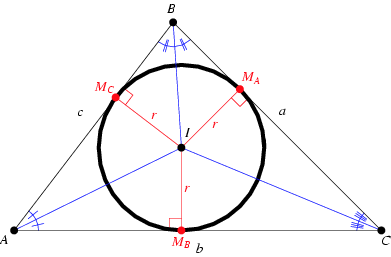
(i)a/sinA = b/sinB = c/sinC = 2R
(ii) p = (a+b+c)/2
(iii) S = 1/2 * ab *sin C ...
S = pr
S^2 = p(p-a)(p-b)(p-c) <---Heron formula
(iv) abc = 4RS
试证明:
p^2 + r^2 + 4Rr = ab + ac + bc
[ 本帖最后由 dunwan2tellu 于 7-4-2006 05:38 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-4-2006 06:00 PM
|
显示全部楼层
要学trigo,必须必备几个基本的恒等式
若 A,B,C 为三角形 ABC 的内角,则
(i) cos A/2 = sqrt{ p(p-a)/bc }
(ii) sin A/2 = sqrt{(p-b)(b-c)/bc}
(iii)tan A/2 = sqrt{(p-b)(p-c)/p(p-a)} = r/(p-a)
(iv) Sum sin A=4cosA/2*cosB/2*cosC/2
(v)Sum sin2A = 4sinA*sinB*sinC
(vi)Sum cosA=1+4sinA/2*sinB/2*sinC/2
(vii)Sum cos2A=-1-4cosA*cosB*cosC
(viii)Sum (cosA)^2 = 1 - 2cosA*cosB*cosC
(ix)Sum (sinA)^2 = 2 + 2cosA*cosB*cosC
(x)Sum tanA = tanA*tanB*tanC
(xi)Sum cotA*cotB = 1
(xii)Sum cotA/2 = cotA/2*cotB/2*cotC/2
附加:
a) sin x + sin y + sin z - sin(x+y+z) = 4sin{(x+y)/2}*sin{(x+z)/2}*sin{(y+z)/2}
b)cos x+ cos y+ cos z - cos(x+y+z)=4cos{(x+y)/2}*cos{(x+z)/2}*cos{(y+z)/2}
那些有兴趣证明这些 identity 的朋友,随时欢迎! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-4-2006 08:01 PM
|
显示全部楼层
发表于 6-4-2006 08:01 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-4-2006 07:30 AM
|
显示全部楼层
发表于 7-4-2006 07:30 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 7-4-2006 01:42 PM
|
显示全部楼层
sum 是 和的意思。
Ex : Sum sinA = sin A + sin B + sin C
我只是些缩写而以... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 7-4-2006 05:34 PM
|
显示全部楼层
补充:
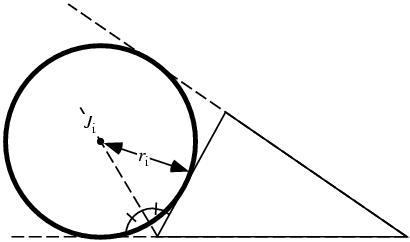
r_a , r_b , r_c 为三角形 ABC 的 exradii,则
(i)r_a + r_b + r_c = 4Rr + r
(ii)r_a x r_b + r_a x r_c + r_b x r_c = p^2
(iii)r x r_a x r_b x r_c = S^2
R = circumradius , r = inradius , p = semiperimeter , S = area ABC
[ 本帖最后由 dunwan2tellu 于 7-4-2006 05:39 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 5-5-2006 06:23 PM
|
显示全部楼层
几何求角度题:
ABCD 是正方形。 E 是 ABCD 内的一点, F 是 ABCD 外的一点,使到 三角形 ABE 和 CBF 全等(congruent)。若 EF = AB , <BFD = 90 , 求 <EBA = ?
提示:想办法先证明三角形 BEF 是等腰直角三角形 。
[ 本帖最后由 dunwan2tellu 于 6-5-2006 05:50 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-5-2006 05:53 PM
|
显示全部楼层
是否网友都不喜欢几何呢?怎么没人来回贴的....
又一题几何证明题!
ABCD 是正方形。 E 在 BD 上。若 P , Q 分别是 三角形 ABE 和 ADE 的外围圆心(circumcenter) , 求证 APEQ 也是 正方形。

[ 本帖最后由 dunwan2tellu 于 6-5-2006 05:54 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|