|
|
 发表于 12-11-2004 09:21 AM
|
显示全部楼层
发表于 12-11-2004 09:21 AM
|
显示全部楼层
12/11/2004,星期五
高中 (B38)
a,b 是 x^2 - (k-1)x + (k^2 + 3k +4)=0
的两根,k 是某些实数。
求 a^2 + b^2 的最大值。 (待解)
(答案:)
(解对者:)
========================================
x^2 - (k-1)x + (k^2 + 3k +4)=0
∵k是實數
∴判別式=(k - 1)^2 - 4(k^2 + 3k + 4)≧0
解得 -3≦k≦-5/3
a^2 + b^2 =(a+b)^2 - 2ab
=(k-1)^2 - 2(k^2 + 3k +4)
=-(k+4)^2 + 9 (過程不寫啦,配方法誰都會)
要讓a^2 + b^2最大=>讓|k+4|最小
∴k=-3時,a^2 + b^2有最大值8
羊按:不知道解得對不對
因為k=-3釋方程式有等根
而a^2+b^2≧2ab
應該a=b時,a^2+b^2有最小值...>"< |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-11-2004 11:07 AM
|
显示全部楼层
灰羊 于 12-11-2004 08:57 AM 说 :
11/11/2004,星期四
高中 (B37)
f 和 g 是两个多项式(polynomial),且
f(x + g(y))=3x + y + 4
给所有实数x,y
求 g( 8 + f (3)) 之值。
(待解)
(答案:)
(解对者:)
======================= ...
设 x 是一个变数,具有下列形式的代数式
a_n x^n +a_n-1 x^(n-1) + ... + a_0
叫做变数 x 的多项式。
参考 http://mathworld.wolfram.com/Polynomial.html |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 11:15 AM
|
显示全部楼层
发表于 12-11-2004 11:15 AM
|
显示全部楼层
如果是這樣,那
f(x + g(y))=3x + y + 4
3x是(x + g(y))裡面的x出來的,
y是(x + g(y))裡面的g(y)出來的 對吧? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 12:37 PM
|
显示全部楼层
发表于 12-11-2004 12:37 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-11-2004 01:00 PM
|
显示全部楼层
a,b 是是实数好了!
灰羊解法对了!
试试星期四的吧!
[ Last edited by 多普勒效应 on 12-11-2004 at 01:03 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 01:49 PM
|
显示全部楼层
发表于 12-11-2004 01:49 PM
|
显示全部楼层
(1)若兩根a、b為任意數
a^2 + b^2 =(a+b)^2 - 2ab
=(k-1)^2 - 2(k^2 + 3k +4)
=-(k+4)^2 + 9 ≦9
故 a^2 + b^2 的最大值是9
(2)若兩根a、b為任意實數
∵兩根a、b為任意實數
∴判別式=(k - 1)^2 - 4(k^2 + 3k + 4)≧0
解得 -3≦k≦-5/3
又a^2 + b^2 =(a+b)^2 - 2ab
=(k-1)^2 - 2(k^2 + 3k +4)
=-(k+4)^2 + 9
則81/9≦(a^2 + b^2)≦8
故 a^2 + b^2 的最大值是8 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 08:35 PM
|
显示全部楼层
发表于 12-11-2004 08:35 PM
|
显示全部楼层
還是不太明白
既然是多項式怎麼沒有x^2之類的.... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 08:39 PM
|
显示全部楼层
发表于 12-11-2004 08:39 PM
|
显示全部楼层
430201 于 12-11-2004 13:49 说 :
(1)若兩根a、b為任意數
a^2 + b^2 =(a+b)^2 - 2ab
=(k-1)^2 - 2(k^2 + 3k +4)
=-(k+4)^2 + 9 ≦9
故 a^2 + b^2 的最大值是9
(2)若兩根a、b為任意實數
∵兩根a、b為任意實數
∴判別 ...
81/9≦(a^2 + b^2)≦8 <===應該是130/9≦(a^2 + b^2)≦8吧 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 09:14 PM
|
显示全部楼层
发表于 12-11-2004 09:14 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 10:15 PM
|
显示全部楼层
发表于 12-11-2004 10:15 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-11-2004 10:52 PM
|
显示全部楼层
厉害
以免大家星期六太闷:-P
小弟贴多一题数论题:
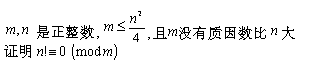 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-11-2004 08:00 PM
|
显示全部楼层
发表于 13-11-2004 08:00 PM
|
显示全部楼层
flash 于 5-11-2004 14:04 说 :
数学训练 - 大专
今天是暂时接过 pipi 网友的棒子贴上大专的数学题目,在此谢谢多坛主的信任,希望各位网友多多的捧场。第一题就试试这个无数题吧 (没有数字资料的题目):
大专 (C12)
一间工厂生产两种口味的糖果:草莓和香草。我们无法从糖果的表面判断糖果的口味。有关的糖果将会包装成包裹。每种包裹里的组合都可能不一样(可能整包都是草莓口味的糖果或是整包都是香草口味的糖果,或是一颗草莓其余香草等等)。假设每包糖果的数量都一样以及每种组合的机率都一样。
小明买了一包有关的糖果,尝了一颗发觉是草莓口味。如果现在小明取第二颗糖果(第一颗没放回去),请问第二颗糖果是草莓口味的机率是多少?
(答案:2/3)
(解对者:sinchee, 萧晨)
大专 (C13)
证明 2≤(1 + 1/n)^n <3
如果 n 是任何 natural numbers.
(不懂有人贴过这问题没有,如有麻烦告诉我, 谢谢)
(解对者:灰羊, 萧晨)
由于长假的关系,所以原本应该周末才贴的题名今天就贴了上来。
大专 (C14)
这题须要有一些赌博的知识,希望不会教坏小孩。
五个赌徒分别坐在五个赌桌玩 poker (也叫 "派"(pair))。如果五个人手上的牌分别是:
(A) A(黑桃)A(红心)A(方块)K(黑桃)K(红心)
(B) A(黑桃)A(红心)A(方块)Q(黑桃)Q(梅花)
(C) A(黑桃)A(红心)A(方块)Q(黑桃)Q(红心)
(D) A(黑桃)A(红心)A(方块)6(黑桃)6(梅花)
(E)A(黑桃)A(红心)A(方块)6(黑桃)6(梅花)
那谁赢的机会最大?(假设是用 52 张牌,没有 joker)
大专 (C15)
请算出
(cos x)^2 + (cos 2x)^2 + ... (cos nx)^2
是多少?
大家都沒注意到FLASH已經出了很多題目...
而且有的也解了
多普勒更新一下吧
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-11-2004 11:21 AM
|
显示全部楼层
发表于 16-11-2004 11:21 AM
|
显示全部楼层
15/11/2004,星期一
初中 (A37)
证明
(待解)
(答案:)
(解对者:)
(sinx)^10+(cosx)^10=[(sinx)^5+(cosx)^5]^2-2(sinx)^5(cosx)^5
=[(sinx)^5+(cosx)^5]^2-1/16(sin2x)^5
已知[(sinx)^5+(cosx)^5]^2>=0,当x为任何常数..
那么
(sinx)^10+(cosx)^10+1/16(sin2x)^5>=0
Aiyo...太久没做数学题了...请问该怎样继续呢??? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-11-2004 07:36 PM
|
显示全部楼层
发表于 16-11-2004 07:36 PM
|
显示全部楼层
我的学校开始考试了。。。
好辛苦
可能会有两个礼拜不能上来了。。
这段期间的练习
帮我留住哟
谢谢 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-11-2004 08:57 PM
|
显示全部楼层
发表于 16-11-2004 08:57 PM
|
显示全部楼层
原式=|a-b-c|+|b-c-a|+|c-a-b|
=-(a-b-c)-(b-c-a)-(c-a-b)
(∵a-b<c,b-c<a,c-a<b)
=-a+b+c-b+c+a-c+a+b
=a+b+c |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-11-2004 02:17 PM
|
显示全部楼层
发表于 18-11-2004 02:17 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-11-2004 04:13 PM
|
显示全部楼层
发表于 18-11-2004 04:13 PM
|
显示全部楼层
高中 (B39)
simplified (5r+2)/r(r+1)(r+2)
===>5r/r(r+1)(r+2) + 2/r(r+1)(r+2)
= 5/(r+1)(r+2) + 2/r(r+1)(r+2)----〉做法在下面
= 5[1/(r+1) - 1/(r+2)] + 2[1/r - 1/(r+1)] - [1/r - 1/(r+2)]
然后summation
=5{1/2-1/102} + 2{1/1-1/101} - {1/1+1/2-1/101-1/102}
=125/51 + 200/101 - 7625/5151
=15200/5151
(不知道有没有粗心,不过做法就是长。。。)
另外simplify 1/r(r+1)(r+2)
===>[1/r] [1/(r+1)(r+2)]
===>[1/r] [1/(r+1) - 1/(r+2)]
===>[1/r(r+1)] - [1/r(r+2)]
===>[1/r - 1/(r+1)] - [1/r - 1/(r+2)]/2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-11-2004 10:34 PM
|
显示全部楼层
发表于 18-11-2004 10:34 PM
|
显示全部楼层
(1)a=1,b=1,c=1~9
a=1,b=2,c=2~9
----------
a=1,b=9,c=9
共:9+8+7+…+1=45(個)
(2)a=2,b=2,c=2~9
a=2,b=3,c=3~9
----------
a=2,b=9,c=9
共:8+7+6-…+1=35(個)
-------------
(8)a=8,b=8,c=8、9
a=8,b=9,c=9
共:2+1=3(個)
(9)a=9,b=9,c=9
共:1(個)
合計=45+36+28+21+15+10+6+3+1=165(個) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-11-2004 10:50 PM
|
显示全部楼层
发表于 18-11-2004 10:50 PM
|
显示全部楼层
設N的末二位數為B,其餘為A
則N=100A+B
N^2=10000A^2+2×100A×B+B^2-----(1)
即B^2的末二位數為04
設B=(ab),顯然b=2或8
一)若b=2
B^2=100a^2+40a+4
得a=0或5
1)a=0→B=02,代入(1),得A的最小值為15,即N的最小值為1502
2)a=5→B=52,代入(1),得A為分數,故無解。
二)若b=8
B^2=100a^2+160a+64
得a=4或9
1)a=4→B=84,代入(1),得A為分數,故無解。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-11-2004 10:51 PM
|
显示全部楼层
发表于 18-11-2004 10:51 PM
|
显示全部楼层
430201 于 18-11-2004 22:50 说 :
設N的末二位數為B,其餘為A
則N=100A+B
N^2=10000A^2+2×100A×B+B^2-----(1)
即B^2的末二位數為04
設B=(ab),顯然b=2或8
一)若b=2
B^2=100a^2+40a+4
得a=0或5
1)a=0→B= ...
2)a=9→B=94,代入(1),得A為分數,故無解。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|