|
|

楼主 |
发表于 15-12-2006 11:15 PM
|
显示全部楼层
bomber27 的解答
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 15-12-2006 11:17 PM
|
显示全部楼层
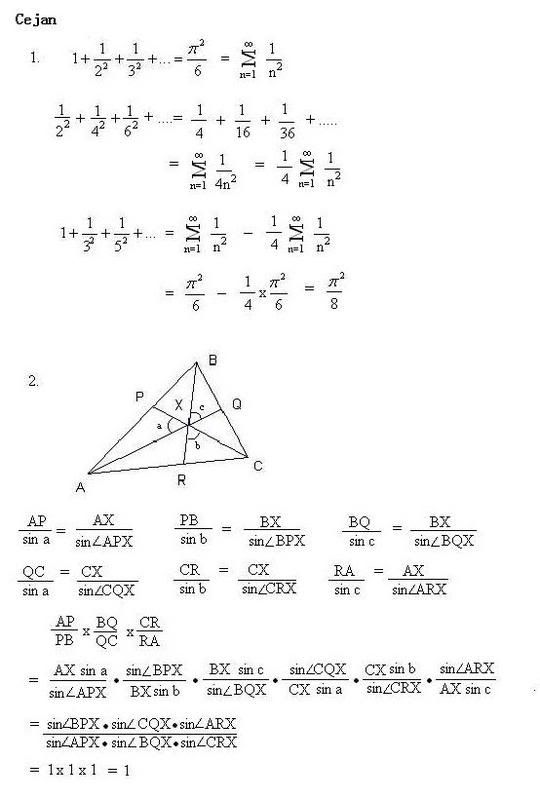
Cejan 的解答
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-12-2006 09:20 PM
|
显示全部楼层
本月第一名为 chiaweiwoo1
第二名为 sardinecan
第三名为 kimsiang
安慰奖: bomber27, cejan
恭喜各位得奖者!
由于第五题我没说清楚实数解或是包括复数解,
所以只回答实数解的参赛者也可得满分。
[ 本帖最后由 多普勒效应 于 17-12-2006 02:08 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-12-2006 11:10 PM
|
显示全部楼层
发表于 16-12-2006 11:10 PM
|
显示全部楼层
|
第5题多普勒效应有一个很完美的解答,可以贴出来吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-12-2006 11:18 PM
|
显示全部楼层
发表于 16-12-2006 11:18 PM
|
显示全部楼层
|
怎么没看到第4题的解答。我知道的是用 graph 来看的,不知道还有另一个解吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-12-2006 11:50 PM
|
显示全部楼层
发表于 16-12-2006 11:50 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 16-12-2006 11:18 PM 发表
怎么没看到第4题的解答。我知道的是用 graph 来看的,不知道还有另一个解吗?
第四题 cejan网友不是已经解了吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-12-2006 11:52 PM
|
显示全部楼层
发表于 16-12-2006 11:52 PM
|
显示全部楼层
原帖由 bomber27 于 16-12-2006 11:50 PM 发表
第四题 cejan网友不是已经解了吗?
好像不完整,而且不大对。
第一,如何得知 a = 2 - (b+c) >= 0 (我看不到)
第二,如何得知 ab >= a (有给吗?)
[ 本帖最后由 dunwan2tellu 于 16-12-2006 11:54 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 12:58 AM
|
显示全部楼层
发表于 17-12-2006 12:58 AM
|
显示全部楼层
原帖由 bomber27 于 16-12-2006 11:50 PM 发表
第四题 cejan网友不是已经解了吗?
我解得乱七八糟, 根本不完整 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 02:01 PM
|
显示全部楼层
发表于 17-12-2006 02:01 PM
|
显示全部楼层
第四题:a+b=2-c--------------(1)
ab+c(a+b)=1
ab=1-c(2-c)=1-2c+c^2---------------------(2)
(1)^2-4*(2)
(a+b)^2-4ab=(a-b)^2≥0
(2-c)^2-4(1-2c+c^2)≥0
-3c^2+4c≥0
所以0≤c≤4/3。
以此类推,0≤a≤4/3,0≤b≤4/3。
设abc=k, a,b,c 是x^3-2x^2+x-k=0的三个根。
设y=x^3-2x^2+x-k
dy/dx=3x^2-4x+1
当dy/dx=0, t =1,1/3
以graph来看,1/3≤b≤1
因为a≥b≥c,所以0≤a≤1/3≤b≤1≤c≤4/3。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 17-12-2006 02:06 PM
|
显示全部楼层
好的好的,现在就贴 ^^
以下是小弟第五题的解答 ;-)
颇为"整洁" 的!
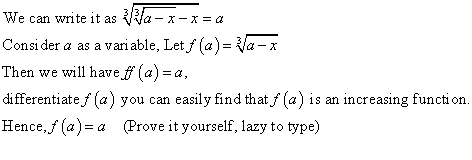
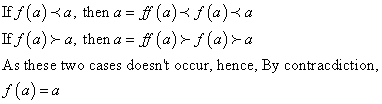 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 17-12-2006 07:05 PM
|
显示全部楼层
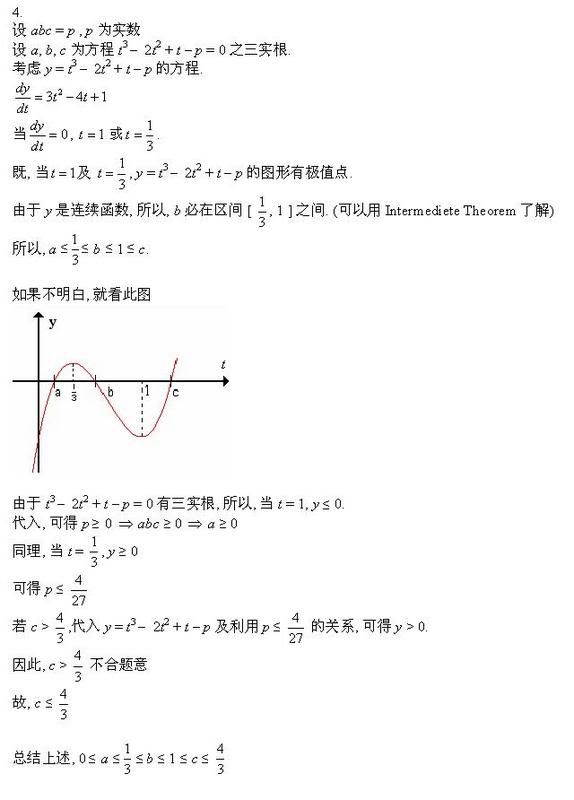
这是我第四题的解答,和chiaweiwoo1的差不远!
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 07:30 PM
|
显示全部楼层
发表于 17-12-2006 07:30 PM
|
显示全部楼层
我有一点问题.........
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 17-12-2006 08:12 PM
|
显示全部楼层
韦达定理:
若 x^3 + ax^2 + bx + c = 0 的三根为 p, q, r.
则
p + q + r = -a
pq + qr + pr = b
pqr = -c |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 10:35 PM
|
显示全部楼层
发表于 17-12-2006 10:35 PM
|
显示全部楼层
原帖由 多普勒效应 于 17-12-2006 08:12 PM 发表
韦达定理:
若 x^3 + ax^2 + bx + c = 0 的三根为 p, q, r.
则
p + q + r = -a
pq + qr + pr = b
pqr = -c
韦达定理英文叫什么? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 10:55 PM
|
显示全部楼层
发表于 17-12-2006 10:55 PM
|
显示全部楼层
原帖由 cejan 于 17-12-2006 10:35 PM 发表
韦达定理英文叫什么?
Viete's theorem。
(x-p)(x-q)(x-r)=0
x³-(p+q+r)x²+(pq+qr+pr)x -pqr =0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 11:00 PM
|
显示全部楼层
发表于 17-12-2006 11:00 PM
|
显示全部楼层
原帖由 bomber27 于 17-12-2006 10:55 PM 发表
Viete's theorem。
(x-p)(x-q)(x-r)=0
x³-(p+q+r)x²+(pq+qr+pr)x -pqr =0
没有学过.......这包括在现在的中学数学课程里吗?
还是从课外读物学到的? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 11:13 PM
|
显示全部楼层
发表于 17-12-2006 11:13 PM
|
显示全部楼层
原帖由 cejan 于 17-12-2006 11:00 PM 发表
没有学过.......这包括在现在的中学数学课程里吗?
还是从课外读物学到的?
中学就有学了吧,只不过刚刚才知道这叫 Viete's theorem
- Viete’s theorem. A sum of roots of reduced quadratic equation x2+ px + q = 0 is equal to coefficient at the first power of unknown, taken with a back sign, i.e.
- x1 + x2 = – p ,
- and a product of the roots is equal to a free term, i.e.
- x1 · x2 = q .
-
[ 本帖最后由 bomber27 于 17-12-2006 11:14 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-12-2006 11:47 PM
|
显示全部楼层
发表于 17-12-2006 11:47 PM
|
显示全部楼层
原帖由 bomber27 于 17-12-2006 11:13 PM 发表
中学就有学了吧,只不过刚刚才知道这叫 Viete's theorem
有吗? 很早就有了吗?
是国中还是独中? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-12-2006 12:25 AM
|
显示全部楼层
发表于 18-12-2006 12:25 AM
|
显示全部楼层
原帖由 cejan 于 17-12-2006 11:47 PM 发表
有吗? 很早就有了吗?
是国中还是独中?
国中中四吧。
y=ax²+bx+c 有两个root, p和q
那 b/a = -(p+q), c/a=pq |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-12-2006 10:39 AM
|
显示全部楼层
发表于 18-12-2006 10:39 AM
|
显示全部楼层
原帖由 bomber27 于 18-12-2006 00:25 发表
国中中四吧。
y=ax²+bx+c 有两个root, p和q
那 b/a = -(p+q), c/a=pq
二次方程的高中二就学了
可是三次方程的根本没有学过   |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|