|
查看: 3091|回复: 46
|
Laplace transform 挑战
[复制链接]
|
|
|
 发表于 10-11-2005 11:31 PM
|
显示全部楼层
发表于 10-11-2005 11:31 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-11-2005 11:56 PM
|
显示全部楼层
原帖由 fadeev_popov 于 10-11-2005 11:31 PM 发表
厉害厉害
这里果然臥虎藏龍
謝謝你
希望你还可以継续尝試一下  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-11-2005 03:30 AM
|
显示全部楼层
发表于 11-11-2005 03:30 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 11-11-2005 08:08 AM
|
显示全部楼层
fadeev_popov 同学
你真的很厉害
我想請問几个問题
在第一题中
做么我們可以define f(t)=f(t+tao)=f(t+2tao)=......
因为它是periodic的嗎?
請問上面的是否也包括第三题的solution?
还有
那个square wave图标怎么弄的?
用什么software?
还有
做么s會>0??
"第一题的方程式也可以用来检验答案,方法如下"中的图
做么要从0到 2tao 呢?不可以是到3tao嗎?
是不是要看
f(t)=1, 0<t<tao
=0, tap<t<2tao 而已?
所以就取t=2tao嗎?
第二题的式子为什么可以証回第一题呢?
怎么懂f(t)=1, 0<t<tao
=0, tao<t<2tao 呢?
請問你可以帮我解释一下嗎?
謝謝
[ 本帖最后由 山羊座 于 11-11-2005 08:47 AM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-11-2005 11:06 AM
|
显示全部楼层
发表于 11-11-2005 11:06 AM
|
显示全部楼层
不要再讲我厉害了,这样会令我感到惭愧。
大家交流讨论就好。
在第一题中
做么我們可以define f(t)=f(t+tao)=f(t+2tao)=...
f(t) = f(t + tao)是题目给的。
既然f(t)=f(t + tao),那么,f(A) = f(A + tao).
设A = t + tao,那就得到f(t + tao) = f(t + tao + tao) = f(t + 2tao).
依次类推,就会得到 f(t) = f(t + tao) = f(t + 2tao) = f(t + 3tao) = ...
第三题的graph和第二题的有点不一样。
那个square wave图标怎么弄的?
用什么software?
我用smart draw 6.5画的。
s 不单要 > 0,而且还要够大,以便当 t --> infinity 时,f(t)e^{-st} 能 --> 0,以保证 L{f(t)} 的存在。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 11-11-2005 04:51 PM
|
显示全部楼层
謝謝你的解答
这样一来明白很多了
smart draw6.5可以从网上下載嗎?
沒听过
要打程式的嗎?
第三和第四有头緒了嗎? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-11-2005 05:43 PM
|
显示全部楼层
发表于 11-11-2005 05:43 PM
|
显示全部楼层
第三题的答案应该是显而易见的,
因为有这样的一个theorem:
for A >= 0,
L{H(t-A)} = (1/s)e^{-sA} (没有书在手,希望没有记错)
所以,只要分别设 A = 0, A = tao, A = 2tao, A = 3tao,
就可以找到你要的答案。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 11-11-2005 06:13 PM
|
显示全部楼层
原帖由 fadeev_popov 于 11-11-2005 05:43 PM 发表
第三题的答案应该是显而易见的,
因为有这样的一个theorem:
for A >= 0,
L{H(t-A)} = (1/s)e^{-sA} (没有书在手,希望没有记错)
所以,只要分别设 A = 0, A = tao, A = 2tao, A = 3tao,
就可以找到你要 ...
这样不是跟第二题的答案很像似嗎?
还有
怎样懂第一题也可以由第二题証得? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2005 07:16 PM
|
显示全部楼层
发表于 12-11-2005 07:16 PM
|
显示全部楼层
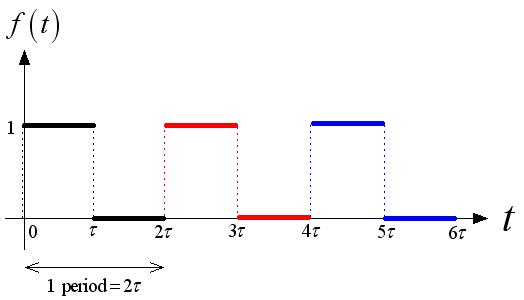
"第一题的方程式也可以用来检验答案,方法如下"中的 t 做么要从 0 到 2tao 呢?不可以是到 3tao 嗎?
是不是要看
f(t) = 1, 0 < t < tao
= 0, tao < t < 2tao 而已,
所以就取 t = 2tao 嗎?
因为 f(t) (那个square wave)就是一个 periodic function with period 2tao. 从图下可以看出,f(t) 一直在重复 0 到 2tao 的本身,所以周期是 2tao.
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2005 07:37 PM
|
显示全部楼层
发表于 12-11-2005 07:37 PM
|
显示全部楼层
第二题的式子并没有証回第一题。
在第一题里,我们用 Lapalace transforms 的定义所得到的 formula 适用于所有的 periodic functions, 而第二题中的 square wave 刚好就是一个周期为 2tao 的 periodic function, 所以那个 formula 当然也适用于它。
怎么懂 f(t) = 1, 0 < t < tao
= 0, tao < t < 2tao 呢?
1)从 f(t) 的 graph 可以看得出来。
2)你尝试把 H(t), -H(t-tao), H(t-2tao), -H(t-3tao), ... 的 graphs 加起来后也可以看得出。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2005 07:47 PM
|
显示全部楼层
发表于 12-11-2005 07:47 PM
|
显示全部楼层
smart draw 6.5 可以从网上下載嗎?
沒听过。
要打程式的嗎?
好像有 7.0 的可以下载,忘记在哪个网址。
第四题我不会解,好像跟专业有关,是 signal processing 吗?还是 control system ? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-11-2005 10:13 PM
|
显示全部楼层
原帖由 fadeev_popov 于 12-11-2005 07:47 PM 发表
好像有 7.0 的可以下载,忘记在哪个网址。
第四题我不会解,好像跟专业有关,是 signal processing 吗?还是 control system ?
我短消息問你的問题你收到了嗎  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-11-2005 12:38 AM
|
显示全部楼层
发表于 13-11-2005 12:38 AM
|
显示全部楼层
在第一题solution中
你展开 L{f(t)}= ... + ... + ...+ ...
在第一项是从 0 到 tao, 第二项是从 tao 到 2tao, ...
接著第一项保留
第二个変成从 0 到 tao
而 f(t)e^{-st} 変成 f(t+tao)e^{-s(t+tao)}
要怎样解释呢?
做么第一项不用変?
第一项不用変是因为我的用意就是要所有的 terms 的 integration limits 都是从 0 到 tao.
而至于 f(t)e^{-st} 変成 f(t+tao)e^{-s(t+tao)} 那是因为:
for t from tao to 2tao, f(t)e^{-st}, ----------------------(1)
可以被写成:
for t from 0 to tao, f(t+tao)e^{-s(t+tao)}. ---------------(2)
(1) 和(2)是一样的,不同写法而已。
把 tao to 2tao 代进 (1)中,得到:
f(tao)e^{-s(tao)} to f(2tao)e^{-s(2tao)}.
把 0 to tao 代进 (2)中,同样,也得到:
f(tao)e^{-s(tao)} to f(2tao)e^{-s(2tao)}.
[ 本帖最后由 fadeev_popov 于 13-11-2005 12:40 AM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 13-11-2005 01:03 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-11-2005 04:30 PM
|
显示全部楼层
发表于 14-11-2005 04:30 PM
|
显示全部楼层
already being solved.... post some more next time...
这已经不是第一次警告。
请用中文发表。
请注意论坛规则。
[ 本帖最后由 多普勒效应 于 14-11-2005 06:08 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-11-2005 11:36 PM
|
显示全部楼层
发表于 14-11-2005 11:36 PM
|
显示全部楼层
第四题:
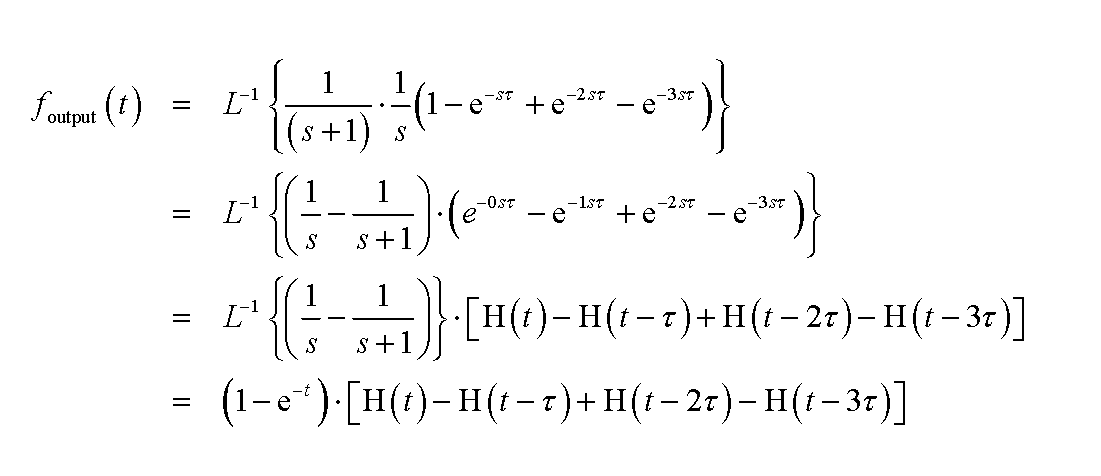 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-11-2005 11:51 PM
|
显示全部楼层
发表于 14-11-2005 11:51 PM
|
显示全部楼层
当 tao = 0.05 时,
f_input:
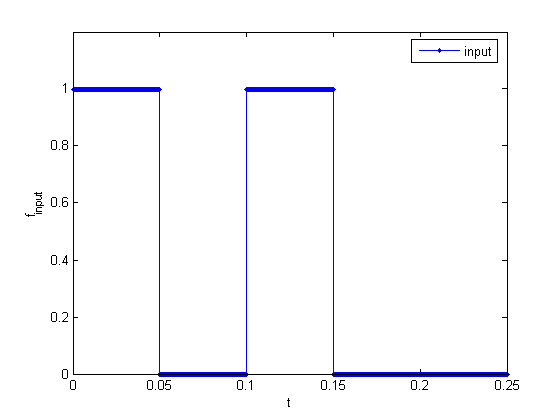
f_output:
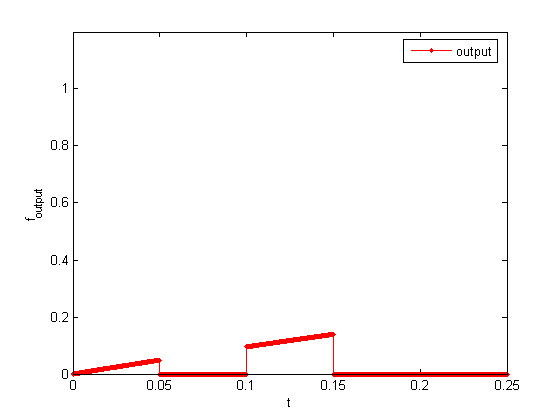 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-11-2005 11:55 PM
|
显示全部楼层
发表于 14-11-2005 11:55 PM
|
显示全部楼层
当 tao = 1 时,
f_input:
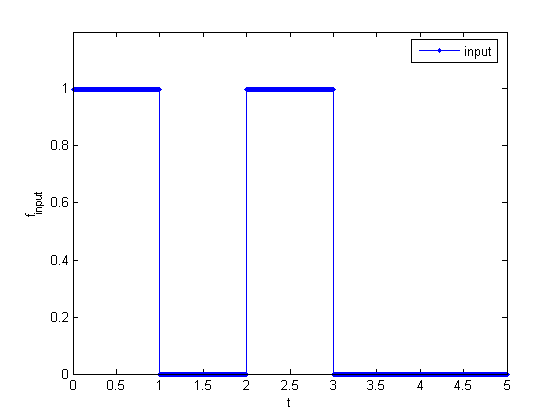
f_output:
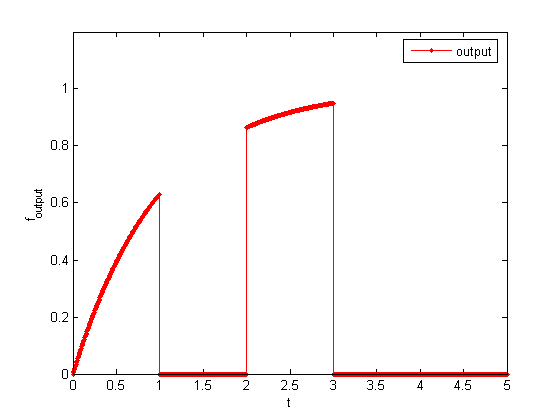 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-11-2005 11:57 PM
|
显示全部楼层
发表于 14-11-2005 11:57 PM
|
显示全部楼层
当 tao = 5 时,
f_input:
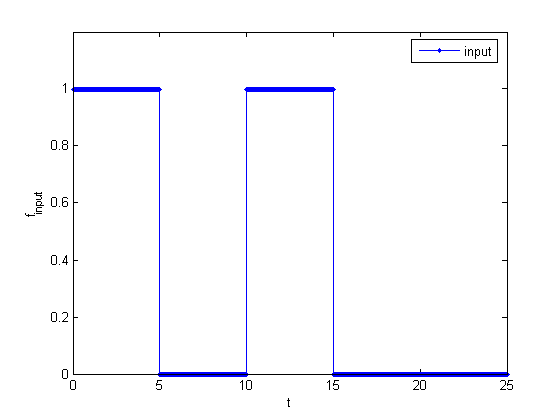
f_output:
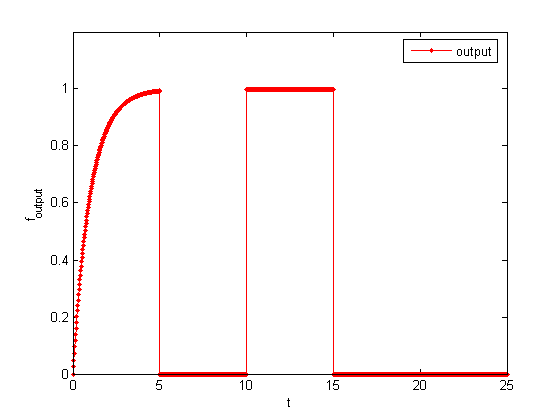 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|