|
查看: 3056|回复: 46
|
高中数学训练题库
 [复制链接]
[复制链接]
|
|
|

楼主 |
发表于 12-10-2004 09:39 AM
|
显示全部楼层
19/08/2004,星期四
高中(B1) 已知 (y+z)/(b+c) = (z+x)/(c+a) = (x+y)/(a+b),
求证 (x+2y-3z)/(4x+5y-6z) = (a+2b-3c)/(4a+5b-6c) (已解)
(答案:--)
(解对者:辉文,sinchee)
解法(一)
x(b+c) + y(c-a) - z(a+b)=0 ---(1)
x(c-b) + y(a+c) - z(a+b)=0 ---(2)
-x(b+c) + y(a+c) + z(a-b)=0 ----(3)
(1) + (3) 得到 2cy-2bz=0
所以 z= cy/b
(1) - (2) 得到 2bx-2ay=0
所以 x = ay/b
好了, 现在把 x, z 代人式子(x+2y-3z)/(4x+5y-6z),即:
= _a/b + 2 -3(c/b)_
4(a/b)+ 5 - 6(c/b)
注意,y已经去掉了,还有同分母去掉 B,就可以证明等於右边的式子
= _(a+2b-3c)_
(4a+5b-6c)
(已证)
解法(二)
设(y+z)/(b+c) = (z+x)/(c+a) = (x+y)/(a+b) = k
则(y+z) = k(b+c) (i)
(z+x) = k(c+a) (ii)
(x+y) = k(a+b) (iii)
(i)+(ii)+(iii), x+y+z = k(a+b+c) (iv)
(iv) - (i), x = ka
(iv) - (ii), y = kb
(iv) - (iii), z = kc
因此(x+2y-3z)/(4x+5y-6z)=(ka+2kb-3kc)/(4ka+5kb-6kc)
=(a+2b-3c)/(4a+5b-6c) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:40 AM
|
显示全部楼层
20/08/2004,星期五
高中(B2) a,b,c,d 为任意正数,设 S = a/(a+b+d) + b/(a+b+c) + c/(b+c+d) + d/(a+c+d)
求证: 1 < S < 2 (已解)
(答案:--)
(解对者:sinchee)
因为a,b,c,d 为任意正数,
a/(a+b+d) > a/(a+b+c+d)
b/(a+b+c) > b/(a+b+c+d)
c/(b+c+d) > c/(a+b+c+d)
d/(a+c+d) > d/(a+b+c+d)
所以
S > a/(a+b+c+d) + b/(a+b+c+d) + c/(a+b+c+d) + d/(a+b+c+d) = 1
而且,
a/(a+b+d) < a/(a+b)
b/(a+b+c) < b/(a+b)
c/(b+c+d) < c/(c+d)
d/(a+c+d) < d/(c+d)
所以
S < a/(a+b) + b/(a+b) + c/(c+d) + d/(c+d) = 2
故 1 < S < 2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:40 AM
|
显示全部楼层
21/08/2004,星期六
高中(B3) 已知 7^82 + 8^161 能被 57 整除,
求证 7^83 + 8^163 也能被 57 整除。 (已解)
(答案:--)
(解对者:fritlizt,强,飞彦)
解法(一)
设 7^82 + 8^161 = k
7^83 + 8^163 = 7^82+(6*7^82) + 8^161+(63*8^161)
=k + 3(2*7^82+21*8^161)
= k + 3(2k + 19*8^161)
= k + 6k + 57*8^161
k 能被57 整除。
所以 k + 6k + 57*8^161 也能被57整除
解法(二)
7^82 + 8^161 被57除
7^83 + 8^163 =7*(7^82)+64*(8^161)=7*(7^82+8^161)+57*(8^161)也被57除 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:42 AM
|
显示全部楼层
26/08/2004,星期四
高中(B4) 求证
(i) 数列 11,111,1111,...
(ii) 数列 44,444,4444,...
中的每一项都不是完全平方数。 (已解)
(答案:--)
(解对者:sinchee)
(i)
设 x^2 = 1111...
则 x必为一奇数,
若 x = 2k + 1
x^2 = 4k^2 + 4k + 1 = 1111...
4(k^2 + k) = 111...110
但,
111...110 不能被4整除
所以1111... 不是完全平方数
(ii)
设 x^2 = 4444...
则 x必为一偶数,
若 x = 2k
x^2 = 4k^2 = 4444...
k^2 = 1111...
因为1111... 不是完全平方数
所以4444... 也不是完全平方数 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:43 AM
|
显示全部楼层
27/08/2004,星期五
高中(B5) 如图,四个一角钱硬币,其中蓝色的沿着其他三个滚了一圈,直到回到原位为止。
请问蓝色的硬币,共转了多少度? (已解)
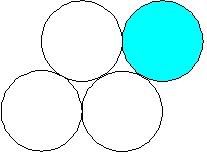
(答案:1080度)
(解对者:微中子,sinchee)
尝试画出来吧,
我是画出来看的.
不懂怎样跟你解释.
转了一次就有360度了.
选一个定的点,比如开始接触的那一点.
转了一边之后,看那一点在哪里,然后乘三就可以了.
希望我讲的明白.
Remark:

看看此图,应该看得出转了一次就是360度了.
看红色点的方向.
有三个, 所以一共3*360. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:43 AM
|
显示全部楼层
28/08/2004,星期六
高中(B6) 设 n (>3) 为自然数且 n, n+2 为质数。
求证 n+1 是 6 的倍数。 (已解)
(答案:--)
(解对者:sinchee)
因为 n, n+2 为质数,
所以 n+1为偶数。
也因为 n, n+2 为质数,不能被3整除,
所以 n+1 能被3整除。
故 n+1 是 6 的倍数。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:55 AM
|
显示全部楼层
2/09/2004,星期四
高中(B7) 若 (1)(1!)+(2)(2!)+(3)(3!)+...+(1001)(1001!) 除以 2004,求其余数。 (已解)
(答案:2003)
(解对者:sinchee)
设
(i) : (1)(1!)+(2)(2!)+(3)(3!)+...+(1001)(1001!)
(ii) : (1!) + (2!) + (3!) + ... + (1001!)
(i) + (ii) : (2)(1!)+(3)(2!)+(4)(3!)+ ... +(1002)(1001!)
= (2!) + (3!) + (4!) + ... + (1002!) -----------(iii)
(i) = (iii) - (ii) = (1002!) - 1
因为(1002!) 可被2004整除,
所以(i) 除以 2004 的余数为2003.
[ Last edited by pipi on 12-10-2004 at 12:00 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:55 AM
|
显示全部楼层
3/09/2004,星期五
高中(B8) 设 0< a < 90(度),sin(a) + cos(a) = sqrt(2)。
求 sin(a) + sin(2a) + ... + sin(8a) 之值。 (已解)
(答案:0)
(解对者:陈敏慧)
解法(一)
sin(3a)= sin(2a+a)=sin(2a)cos(a)+cos(2a)sin(a)=cos(a)=sin(a)
sin(4a)= 2sin(2a)cos(2a)=0
sin(5a)= sin(4a+a)= sin(4a)cos(a)+cos(4a)sin(a)= -sin(a)
sin(6a)= sin(4a+2a)=sin(4a)cos(2a)+cos(4a)sin(2a)= -1
sin(7a)= sin(3a+4a)= sin(3a)cos(4a) +cos(3a)sin(4a)=-sin(3a)=-sin(a)
sin(8a)= 2sin(4a)cos(4a)=0
将 sin(a)+sin(2a)+...+sin(8a)全部加起来也是等於零。
解法(二)
由0< a < 90(度),sin(a) + cos(a) = sqrt(2),我们得知 a = 45度,所以我们有
sin(8-k)a = sin(8a-ka) = -sin(ka)
由此, sin(a) + sin(2a) + ... + sin(8a) = 0 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:56 AM
|
显示全部楼层
4/09/2004,星期六
高中(B9) 若 (a+b)/(a-b) = (b+c)/(2(b-c)) = (c+a)/(3(c-a)),
求证: 8a + 9b + 5c = 0 (已解)
(答案:--)
(解对者:陈敏慧,sinchee)
解法(一)
设 (a+b)/(a-b) = (b+c)/(2(b-c)) = (c+a)/(3(c-a))=k,得到
(a+b)=k(a-b)
(b+c)= 2k(b-c)
(c+a)= 3k(c-a)
所以 8a+9b+5c= 6a+2a+6b+3b+3c+2c
= 6(a+b) + 3(b+c) + 2(a+c)
把 (a+b),(b+c),(c+a)代人进去,得到
8a+9b+5c= 6(k(a-b)) +3(2k(b-c))+ 2(3k(c-a))
= 0
得证,8a+9b+5c=0。
解法(二)
若 (a+b)/(a-b) = (b+c)/(2(b-c)) = (c+a)/(3(c-a)) = k
(i) : (a+b) = k(a-b)
(ii) : (b+c) = 2k(b-c)
(iii) : (c+a) = 3k(c-a)
(i)+(ii)+(iii):a+b+c = -ka + (1/2)kb + (1/2)kc
(iv)-(i) : c = -2ka + (3/2)kb +(1/2)kc
(iv)-(ii) : a = -ka - (3/2)kb + (5/2)kc
(iv)-(iii): b = 2ka + (1/2)kb - (5/2)kc
8a + 9b + 5c = 8[-ka - (3/2)kb + (5/2)kc]
+ 9[2ka + (1/2)kb - (5/2)kc]
+ 5[-2ka + (3/2)kb +(1/2)kc]
= 0 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:58 AM
|
显示全部楼层
9/09/2004,星期四
高中(B10) 若 n 为自然数,求证 n^2 + n + 2 不能被 15 整除。 (已解)
(答案:--)
(解对者:sinchee)
若 n = 3k,
n^2 + n + 2 = 9k^2 + 3k + 2
= 3(3k^2 + k) + 2
= 2(mod3)
若 n = 3k + 1,
n^2 + n + 2 = 9k^2 + 9k + 4
= 3(3k^2 + 3k + 1) + 1
= 1(mod3)
若 n = 3k + 2,
n^2 + n + 2 = 9k^2 + 15k + 8
= 3(3k^2 + 5k + 2) + 2
= 2(mod3)
因此 n^2 + n + 2 不能被 3 整除﹐當然也不能被15整除。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:58 AM
|
显示全部楼层
10/09/2004,星期五
高中(B11) 若 n 为整数,
试将 1 + 1/n^2 + 1/(n+1)^2 可写成 (a/b)^2 的形式,其中 a,b 为整数。 (已解)
(答案:[(n(n+1)+1)/n(n+1)]^2)
(解对者:chwk87,强)
解法(一)
1 + 1/n^2 + 1/(n+1)^2
=(n^2+1)/n^2+ 1/(n+1)^2
=((n+1)^2-2n)/n^2+ 1/(n+1)^2
=((n+1)^2(n+1)^2-2n(n+1)^2+n^2)/n^2(n+1)^2
设 n+1为 x
(x^4-2nx+n^2)/n^2x^2
=(x^2-n)^2/(nx)^2
=(n^2+n+1)^2/(n^2+n)^2
所 以 a=n^2+n+1 and b=n^2+n
已 知 n 为整数,
所 以 a和 b也 是 整数
解法(二)
2n^2+2n+1+n^2(n+1)^2
=n(n+1)^2+2n(n+1)+1
1 + 1/n^2 + 1/(n+1)^2
=1+[(n+1)^2+n^2]/[n^2*(n+1)^2]
=1+(2n^2+2n+1)/(n^2(n+1)^2)
=[(n^2(n+1)^2+2n(n+1)+1]/(n^2(n+1)^2)
=[(n(n+1)+1)/n(n+1)]^2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:58 AM
|
显示全部楼层
11/09/2004,星期六
高中(B12) 把1600粒花生分给100只猴子。
证明:不管怎样分,至少有4只猴子得到的花生一样多。
能否找到一种分法,使得没有5只猴子得到同样多的花生。 (已解)
(答案:--)
(解对者:sinchee)
先来证明:不管怎样分,至少有4只猴子得到的花生一样多。
假设第1到第99只猴子,没有4只猴子得到的花生一样多。
意思是说,最多有3只分得一样多。
最省花生的分法,当然是3只0粒,3只1粒,3只2粒,… ,3只32粒,依此类推。
分完99只猴子后,共分了1584粒。(等差级数)
剩下16粒,分给第100只猴子,
这就有4只猴子得到的花生一样多了。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:07 AM
|
显示全部楼层
16/09/2004,星期四
高中(B13) 下图所示为边长为 1 的正方体。
AC 及 BE 为对角线。P、Q 分别是 AC 及 BE 上的点。
那么 PQ (沿着立方体表面)的最短距离为___。
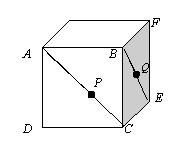 (已解) (已解)
(答案:1/√2)
(解对者:fritlizt)
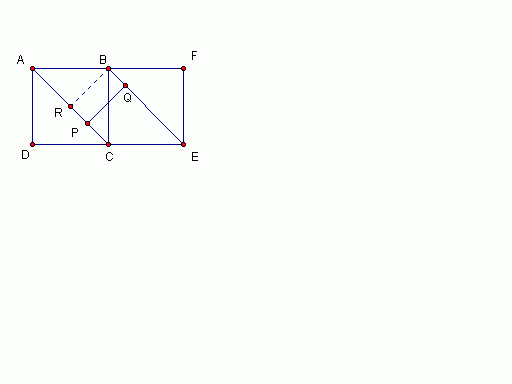
把立方体打开来看。
PQ 最短的距离是当PQ 直角的时候。
PQ = RB
ABCD = 正方形
RB = AR
AR = 1/2 AC
= 1.4142
PQ = 1.4142/2
= 0.7071
[ Last edited by pipi on 12-10-2004 at 11:41 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:07 AM
|
显示全部楼层
17/09/2004,星期五
高中(B14) 图中所示为两个半径为 1 的圆,其中心分别为原点及(1,0)。
求阴影部分的面积(答案以 π 或根号(surd form)来表示)。
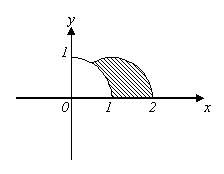 (已解) (已解)
(答案:1/6 π + √3/4)
(解对者:sinchee)
阴影部分的面积
= (120/360) π – [(60/360) π – (1/2)(1)(√3/2)]
= 1/6 π + √3/4
[ Last edited by pipi on 12-10-2004 at 10:18 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:07 AM
|
显示全部楼层
18/09/2004,星期六
高中(B15) 证明:
 (已解) (已解)
(答案:--)
(解对者:sinchee)
当 r=1, 1/r^2 =1,
r>1, 1/r^2>0
所以 ∑1/r^2 > 1
然后。。。请看下图:

[ Last edited by pipi on 12-10-2004 at 11:55 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:10 AM
|
显示全部楼层
23/09/2004,星期四
高中(B16) 若 a,b 为 方程式 x^2 + 6x + 1 = 0 之根,
求 (√a + √b)^2 之值。 (已解)
(答案:- 8)
(解对者:fritlizt)
(a+b) < 0, ab = 1,所以, a ,b < 0 ;
a,b < 0;
√a√b = -√ab
(√a + √b)^2 = (a + b) - 2√ab
= (- 6) - 2(√1)
= - 8
[ Last edited by pipi on 12-10-2004 at 11:50 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:10 AM
|
显示全部楼层
24/09/2004,星期五
高中(B17) 设 {a} 为任意的等差数列,其公差为 d,而且{a}的每一项皆是整数。
若 w,x,y,z 为{a} 连续的四项。
证明:wxyz + d^4 是个完全平方数。 (已解)
(答案:--)
(解对者:止战之殇)
{w,x,y,z} = {m,m+d,m+2d,m+3d}
wxyz + d^4 = (m)(m+d)(m+2d)(m+3d) + d^4
= (m^2 + md)(m^2 + 5md + 6d^2) + d^4
= m^4 + 5dm^3 + 6[(md)^2] + dm^3 + 5[(md)^2] + 6md^3 + d^4
= m^4 + 6dm^3 + 11[(md)^2] + 6md^3 + d^4
= (m^2 + d^2)^2 + 6dm^3 + 6md^3 + 9[(md)^2]
= (m^2 + d^2)^2 + 6md(m^2 + d^2) + 9[(md)^2]
= [(m^2 + d^2) + 3md]^2
[ Last edited by pipi on 12-10-2004 at 11:42 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:10 AM
|
显示全部楼层
25/09/2004,星期六
高中(B18)
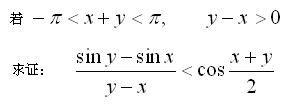 (已解) (已解)
(答案:--)
(解对者:sinchee)

[ Last edited by pipi on 12-10-2004 at 11:48 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:11 AM
|
显示全部楼层
30/09/2004,星期四
高中(B19)
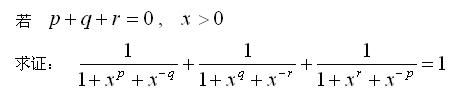 (已解) (已解)
(答案:--)
(解对者:eeCyang,止战之殇)
解法(一)
设x^p=a,x^q=b,x^r=c.
得abc=1 ==> ab = 1/c , bc = 1/a , b = 1/ac
1/(1+x^p+1/[x^q]) + 1/(1+x^q+[1/x^r]) + 1/(1+x^r+[1/x^p])
= 1/(1+a+[1/b]) + 1/(1+b+[1/c]) + 1/(1+c+[1/a])
= b/(b+ab+1) + c/(c+bc+1) + a/(a+ac+1)
= [1/ac]/[(1/ac)+(1/c)+1] + c/[c+(1/a)+1] + a/[a+ac+1]
= [1/ac]/[(1+a+ac)/ac] + c/[(ac+1+a)/a] + a/[a+ac+1]
= [1/ac]*[ ac/(1+a+ac)] + ac/[(ac+1+a)] + a/[a+ac+1]
= 1/[1+a+ac] + ac/[(ac+1+a)] + a/[a+ac+1]
= 1
解法(二)
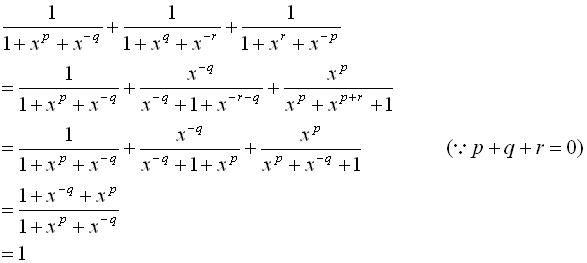
[ Last edited by pipi on 12-10-2004 at 11:56 AM ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|