数学训练（十月份）

初中(A28) 100 个学生排成一列，由左到右，报数！
          1,2,3,...,100。
          现在喊奇数的学生退出；喊偶数的学生保留，然后由左到右，报数！
          1,2,3,...,50。
          现在喊奇数的学生退出；喊偶数的学生保留，然后由左到右，报数！
          1,2,3,...,25。
          。。。
          如此指令重复，直到最后一个学生！
          问：这最后一个学生第一次喊什么号码？

第一次剩下2的倍數：2、4、6、8、…、100
第二次剩下4的倍數：4、8、12、16、…、100
第三次剩下8的倍數：8、16、24、32、…、96
第四次剩下16的倍數：16、32、48、64、80、96
第五次剩下32的倍數：32、64、96
第六次剩下64的倍數：64

pipi

19/10/2004，星期二
初中(A29) 若 1/a  + 1/b + 1/c = 1/(a+b+c),
          求证 1/a^n + 1/b^n + 1/c^n = 1/(a+b+c)^n，其中 n 为奇数。 （待解）
          （答案：）
          （解对者：）

敬请留意：
今早放的问题，不太适合当初中的题目，所以今天的题目改为如下：

19/10/2004，星期二
初中(A29) 若 1/a  + 1/b + 1/c = 1/(a+b+c),
          求证 a^3 + b^3 + c^3 = (a+b+c)^3。 （待解）
          （答案：）
          （解对者：）

多普勒效应

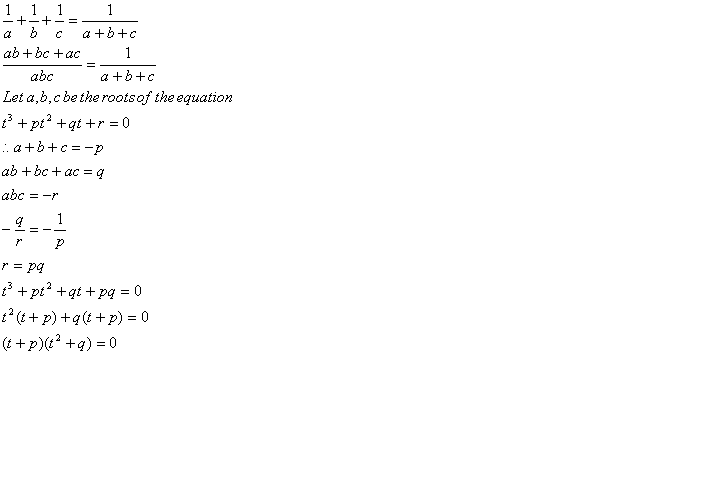
所以，a,b,c 中必有两个是相反数。
设 a=-b
所以
a^3 + b^3 + c^3 = c^3
(a+b+c)^3 = c^3
所以 a^3+b^3+c^3 = (a+b+c)^3

[ Last edited by 多普勒效应 on 19-10-2004 at 03:26 PM ]

已知 1/a  + 1/b + 1/c = 1/(a+b+c),
去分母化簡得a^2×b＋a×b^2＋b^2×c＋b×c^2＋c^2×a＋c×a^2＝－2abc
又(a+b+c)^3＝a^3＋b^3＋c^3＋3(a^2×b＋a×b^2＋b^2×c＋b×c^2＋c^2×a＋c×a^2)＋6abc
得(a+b+c)^3－(a^3 + b^3 + c^3)＝3(a^2×b＋a×b^2＋b^2×c＋b×c^2＋c^2×a＋c×a^2)＋6abc＝3×(－2abc)＋6abc＝0
故a^3 + b^3 + c^3 = (a+b+c)^3

已知 1/a  + 1/b + 1/c = 1/(a+b+c),
去分母化簡得abc＝(a+b+c) (ab+bc+ca)

以a、b、c為三根構造一個x的一元三次方程式：
(x－a)(x－b)(x－c)＝0
展開x^3－(a+b+c)x^2＋(ab+bc+ca)x－abc＝0
則x^3－(a+b+c)x^2＋(ab+bc+ca)x－(a+b+c) (ab+bc+ca)＝0
因式分解得〔x－(a+b+c)〕〔x^2＋(ab+bc+ca)〕＝0
因為a為其一根
所以a－(a+b+c)＝0，即b＝－c
則a^3 + b^3 + c^3 =a^3 + (－c)^3 + c^3 =a^3
   (a+b+c)^3＝(a－c+c)^3=a^3
故a^3 + b^3 + c^3 = (a+b+c)^3

若 abc = 1, 求證： 1/(ab+a+1) + 1/(bc+b+1) + 1/(ac+c+1) = 1

sol：1/(ab+a+1) + 1/(bc+b+1) + 1/(ac+c+1)
   ＝1/(ab+a+1) + a/(abc+ab+a) +ab/(abac+abc+ab)
   ＝1/(ab+a+1) + a/(1+ab+a) + ab/(a+1+ab)（∵abc = 1）
   ＝(ab+a+1)/ (ab+a+1)
   ＝1

若實數 a,b 滿足 0 < a < b 和 a^2 + b^2 = 6ab,
          那麽(a+b)/(a-b) 爲 _______。

∵0 < a < b
∴a+b＞0，a-b＜0
則(a+b)/(a-b)＜0
又﹝(a+b)/(a-b)﹞^2
  ＝(a^2＋2ab＋b^2)/(a^2－2ab＋b^2)
  ＝(a^2＋2ab＋b^2)/(a^2－2ab＋b^2)
  ＝(6ab＋2ab/(6ab－2ab)
  ＝2（∵ a b≠0）
故(a+b)/(a-b)＝－√2

若 a/b = b/c = c/d = d/a ，其中 abcd ≠0。
          求 (a+b+c+d)/(a+b+c-d) 之值。

設 a/b = b/c = c/d = d/a＝k（k為常數）
則a＝bk，b＝ck，c＝dk，d＝ak
即a＝ck^2＝dk^3＝ak^4
∵a≠0，∴k^4＝1→k＝±1
（1）若k＝1
     則a＝b＝c＝d
     故(a+b+c+d)/(a+b+c-d)＝(4a)/(2a)＝2（∵a≠0）
（2）若k＝－1
     則b＝－a，c＝a，d＝－a
     故(a+b+c+d)/(a+b+c-d)＝0/(2a)＝0（∵a≠0）

【修正版】
已知 1/a  + 1/b + 1/c = 1/(a+b+c),
去分母化簡得abc＝(a+b+c) (ab+bc+ca)

以a、b、c為三根構造一個x的一元三次方程式：
(x－a)(x－b)(x－c)＝0
展開x^3－(a+b+c)x^2＋(ab+bc+ca)x－abc＝0
則x^3－(a+b+c)x^2＋(ab+bc+ca)x－(a+b+c) (ab+bc+ca)＝0
因式分解得〔x－(a+b+c)〕〔x^2＋(ab+bc+ca)〕＝0
因為a、b、c為其根
所以a－(a+b+c)＝0，b－(a+b+c)＝0，或c－(a+b+c)＝0，必有一者必成立
（1）若a－(a+b+c)＝0，即b＝－c
則a^3 + b^3 + c^3 =a^3 + (－c)^3 + c^3 =a^3
   (a+b+c)^3＝(a－c+c)^3=a^3
故a^3 + b^3 + c^3 = (a+b+c)^3
（2）若b－(a+b+c)＝0，即a＝－c
或（3）若c－(a+b+c)＝0，即a＝－b
兩者皆同理可證a^3 + b^3 + c^3 = (a+b+c)^3

已知 1/a  + 1/b + 1/c = 1/(a+b+c),去分母得
  (a＋b＋c)(ab＋bc＋ca)＝abc
  ﹝(a＋b)＋c﹞(ab＋bc＋ca)－abc＝0
(a＋b)(ab＋bc＋ca)＋c(ab＋bc＋ca)－abc＝0
(a＋b)(ab＋bc＋ca)＋c^2(a＋b)＝0
(a＋b)(ab＋bc＋ca＋c^2)＝0
(a＋b)﹝b(a＋b)＋c(a＋c)﹞＝0
(a＋b)(b＋c)(c＋a)＝0
則a＝－b或b＝－c或c＝－a
分別以a＝－b或b＝－c或c＝－a代入
   a^3 + b^3 + c^3 = (a+b+c)^3
的左右兩式即得證

多普勒效应

20/10/2004，星期三
初中(A30)

推理方法 ^^"  :-P  好像很罗嗦~~

借用樓上的A、B、C、D、E、F、G、H、I，謝謝！！

∵(A＋D＋G)＋(D＋E＋F)＝23＋21＝44
又A＋D＋G＋E＋F的最大值為(9＋8＋7＋6＋5＝)35
∴D＝9，且A、G、E、F必為5、6、7、8之一。
而B、C、H、I必為1、2、3、4之一。

∵C＋F＋I＝8，且F為5、6、7、8之一  C、I為1、2、3、4之一。
∴F＝5，則E＝21－9－5＝7，

史奴比{^_^}

20/10/2004，星期三
初中(A30) 小明将 1,2,3,4,5,6,7,8,9 分别写在3X3的表格内（如下图），每格一个数字。
          他分别将各（横）行，和各（竖）列的三个数加起来。
          把和写在表的下方和右方。
          试找出 * 之值。
           

答案 ：   先找出最大的和数。
         
         23 = 9 + 8 + 6  （只有唯一的选择）
         21 = 9 + 7 + 5    或者  8 + 7 + 6

        但是 若用 8 + 7 + 6， 那么将会出现两个数字重复，
        所以 只有 21 = 9 + 7 + 5

        9 将会重叠， 所以9 一定要在上中间。

        
       ** 不要意思，早上要上班了，赶着写答案， 让我继续解释

       别那么怪我嘛 。。   。。 这题我在1分钟内解出来的啊。**

        
       现在 7 和 5 的位置 就要考虑放在哪里。
       若把 5 放中间，那么

       14 = 8 + 5 + 1  / 7 + 5 + 2 / 6 + 5 + 3 / 4 + 5 + 6 /      

       6，7，8，9 已经用过了
       那么看来以上的都不可以用。
       所以只有 7 可以摆中间。
      
       1， 2， 3， 4， 就如以下添进去


          8    9    6  |    23
          4    7    3  |    14
          1    5    2  |    8
        -----------------------  
          13   21   11

        * 当然是 7。     

  酱解释可以吗？？？   

[ Last edited by 史奴比{^_^} on 21-10-2004 at 04:00 PM ]

□試著探討樓上先進的解題過程：

23 = 9 + 8 + 6───正確
雖然 21 = 9 + 7 + 5有可能，但21＝8＋7＋6也是否該討論其為何不成立？

又如果只討論到這一步驟，只能得知所求的數為5或7
要確定所求的數為7，那還得再繼續討論下去。

□或許樓上的先進是有意省略，但我覺得很容易誤導！故願意在此畫蛇添足一番！

第一次剩下2的倍數：2、4、6、8、…、100（50個）
第二次剩下型如2＋4n的數：2、6、10、14、…、98（25個）
第三次剩下型如6＋8n的數：6、14、22、30、…、94（12個）
第四次剩下型如6＋16n的數：6、22、38、54、70、86（6個）
第五次剩下：22、54、86
第六次剩下：54

pipi

21/10/2004，星期四
高中(B28) 我们设
          指令（1）为：由左到右，报数! 喊奇数的学生退出；喊偶数的学生保留，
          指令（2）为：由右到左，报数! 喊奇数的学生退出；喊偶数的学生保留，

          100 个学生排成一列。
          指令（1）
          指令（2）
          指令（1）
          指令（2）
          ...
          如此指令重复，直到最后一个学生！
          问：这最后一个学生第一次喊什么号码？

一些小小的扩展：若一开始有 n 位学生（n 为正整数），然后执行上面指令直到最后一个学生，答案会是怎样呢？

史奴比{^_^}

18/10/2004，星期一
初中(A28) 100 个学生排成一列，由左到右，报数！
          1,2,3,...,100。
          现在喊奇数的学生退出；喊偶数的学生保留，然后由左到右，报数！
          1,2,3,...,50。
          现在喊奇数的学生退出；喊偶数的学生保留，然后由左到右，报数！
          1,2,3,...,25。
          。。。
          如此指令重复，直到最后一个学生！
          问：这最后一个学生第一次喊什么号码？


解答：  先大约说会喊多少次才剩下一个。

n=0   :   1,2 ... 100
n=1   :   1,2 ... 50
n=2   :   1,2 ... 25
n=3   :   1,2 ... 12
n=4   :   1,2 ... 6
n=5   :   1,2,3
n=6   :   1

一共需要六次才剩下一个。

那么让我们看看每次剩下的报数（所显示的是第一次所报的数）

n=1  : 2,4,6 ... 100    (x2的倍数)
n=2  : 4,8,12 ... 100   (x4的倍数)
n=3  : 8,16,24 ... 96   (x8的倍数)
n=4  : 16,32,... 96     (x16的倍数)
n=5  : 32,64,96         (x32的倍数)
n=6  : 64               

我们可以看到每次剩下的数目有一定的formula

总结来说，要得到最后一个报数的“原数”的方程式是 2^n
n=6

所以是 2^6 = 64

多普勒效应

22/10/2004，星期五
高中(B29)

不懂可以吗...


极大值时是当 a=b=0

建议 : 题目可改为找极小值 :-P

[ Last edited by 多普勒效应 on 22-10-2004 at 11:35 PM ]

pipi

22/10/2004，星期五
高中(B29) 若 0< a,b < 1 。
          试求
√{a^2 + b^2} + √{(1-a)^2 + b^2} + √{(1-a)^2 + (1-b)^2} + √{a^2 + (1-b)^2}
          的极小值。 （待解）
          （答案：）
          （解对者：）

抱歉！抱歉！
这一题该是找极小值。
我忙晕了头！！！
我已在第一页做了编辑。。。
谢谢 多普勒效应 的提醒！！

多普勒效应

22/10/2004，星期五
高中(B29)

利用构造法:



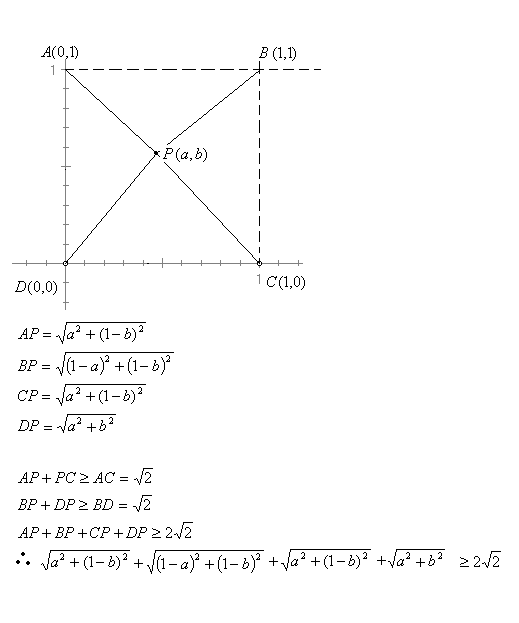
所以,极小值是 2√2

请问,上面那个极大值的解法对吗 ?

[ Last edited by 多普勒效应 on 23-10-2004 at 11:03 AM ]