|
|
 发表于 23-9-2004 02:58 PM
|
显示全部楼层
发表于 23-9-2004 02:58 PM
|
显示全部楼层
[quote] 無聊人 于 03-09-2004 16:20 说 :
你看到你的错误啦?
我看到啦,谢谢。
试试今天 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 03:04 PM
|
显示全部楼层
发表于 23-9-2004 03:04 PM
|
显示全部楼层
奇怪,为什么刚才的贴子不完整的?
试试今天的题目:
若 a,b 为 方程式 x^2 + 6x + 1 = 0 之根,
求 (√a + √b)^2 之值。
a,b 为方程式 x^2 + 6x + 1 = 0 之根,
(x - a)(x - b) = 0
x^2 - (a + b)x + ab = 0
-(a + b) = 6 ==> a + b = - 6
ab = 1
(√a + √b)^2 = (a + b) + 2√ab
= (- 6) + 2(√1)
= - 4
这次没掉入陷阱吧? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-9-2004 03:09 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 03:29 PM
|
显示全部楼层
发表于 23-9-2004 03:29 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 04:08 PM
|
显示全部楼层
发表于 23-9-2004 04:08 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 04:08 PM
|
显示全部楼层
发表于 23-9-2004 04:08 PM
|
显示全部楼层
止战之殇 于 23-9-2004 03:04 PM 说 :
(√a + √b)^2 = (a + b) + 2√ab
= (- 6) + 2(√1)
= - 4
(a+b) < 0, ab = 1,所以, a ,b < 0 ;
a,b < 0;
√a√b = -√ab
(√a + √b)^2 = (a + b) - 2√ab
= (- 6) - 2(√1)
= - 8
[ Last edited by fritlizt on 23-9-2004 at 04:10 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 04:47 PM
|
显示全部楼层
发表于 23-9-2004 04:47 PM
|
显示全部楼层
我还是觉得不对.
(/a+/b)^2 < 0 , 不可能会有副号. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 06:46 PM
|
显示全部楼层
发表于 23-9-2004 06:46 PM
|
显示全部楼层
史奴比{^_^} 于 23-9-2004 04:47 PM 说 :
我还是觉得不对.
(/a+/b)^2 < 0 , 不可能会有副号.
什么是副号?? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-9-2004 08:23 PM
|
显示全部楼层
史奴比{^_^} 于 23-9-2004 12:50 PM 说 :
哇.. 原来这里有酱的一个论坛,我却没发现.
我好久没动数学题了.
pipi坛主,现在有什么题还没解的?
请看这主题的第一页!!
fritlizt 于 23-9-2004 06:46 PM 说 :
什么是副号??
我想 史奴比{^_^} 要说的是"负号"吧!!
"负号"是 negative sign.
史奴比{^_^},请参考:
强 于 23-9-2004 03:29 PM 说 :
x^2>=0, x是实数
fritlizt 于 23-9-2004 04:08 PM 说 :
(a+b) < 0, ab = 1,所以, a ,b < 0 ;
a,b < 0;
√a√b = -√ab
fritlizt,果然不错!!
[ Last edited by pipi on 23-9-2004 at 08:30 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-9-2004 09:16 PM
|
显示全部楼层
终结一下 (待解) 的问题。
16/09/2004,星期四
高中(B13) 下图所示为边长为 1 的正方体。
AC 及 BE 为对角线。P、Q 分别是 AC 及 BE 上的点。
那么 PQ (沿着立方体表面)的最短距离为___。
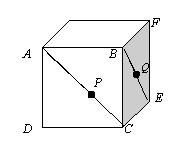 (待解) (待解)
19/09/2004,星期日
大专(C5) 某个醉汉目前在位置 "5",他的家在位置 "8",而位置 "0" 则是断崖。
由于他分不清方向,设他每次移动一单位,且只走向左或向右,而每次向左或向右的机率皆为 1/2。
若到位置 "8",则家人迎接他(安全抵达)。
若到位置 "0", 则跌入断崖。。。(无法继续行程)
求此醉汉安全回到家的机率。
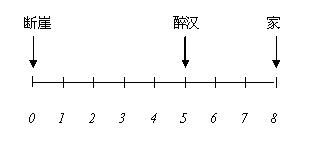 (待解) (待解)
21/09/2004,星期二
初中(A17) A 是含有 21 数字的偶数。
已知 A 是完全平方数,及 A 的十位数为 6。
那么 A 的个位数则为__。 (待解)
可以的话,先解了以上的问题!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 10:18 PM
|
显示全部楼层
发表于 23-9-2004 10:18 PM
|
显示全部楼层
pipi 于 23-9-2004 09:16 PM 说 :
终结一下 (待解) 的问题。
可以的话,先解了以上的问题!!
高中(B13)
答案是不是 0.7071???? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 11:25 PM
|
显示全部楼层
发表于 23-9-2004 11:25 PM
|
显示全部楼层
fritlizt 于 23-9-2004 22:18 说 :
高中(B13)
答案是不是 0.7071????
我也是算到0.7071.. ! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-9-2004 08:57 AM
|
显示全部楼层
fritlizt 于 23-9-2004 10:18 PM 说 :
高中(B13)
答案是不是 0.7071???? 史奴比{^_^} 于 23-9-2004 11:25 PM 说 :
我也是算到0.7071.. !
请写出解法,让大家参考参考!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 10:01 AM
|
显示全部楼层
发表于 24-9-2004 10:01 AM
|
显示全部楼层
let's say : PQ = z , CE = x , DC = y
Z = ( x^2 + y^2 ) ^ (1/2)
所以,若要Z最短, X 和 Y 一定要 0.5.
(0.5^2 + 0.5^2)^(1/2) = 0.7071
对吗? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-9-2004 11:03 AM
|
显示全部楼层
史奴比{^_^} 于 24-9-2004 10:01 AM 说 :
let's say : PQ = z , CE = x , DC = y
Z = ( x^2 + y^2 ) ^ (1/2)
所以,若要Z最短, X 和 Y 一定要 0.5.
(0.5^2 + 0.5^2)^(1/2) = 0.7071
对吗?
若你设 CE = x , DC = y ,
如图所示:
下图所示为边长为 1 的正方体。

即 x = y = 1 (x,y 已不是变量(variable))
。。。
这讲法不对!
Z = ( x^2 + y^2 ) ^ (1/2)
所以,若要Z最短, X 和 Y 一定要 0.5.
这句话也不对!!
[ Last edited by pipi on 24-9-2004 at 11:06 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 11:15 AM
|
显示全部楼层
发表于 24-9-2004 11:15 AM
|
显示全部楼层
那么我应该说
CE'= X , DC'= Y
那么就是variable. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-9-2004 11:25 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 11:31 AM
|
显示全部楼层
发表于 24-9-2004 11:31 AM
|
显示全部楼层
投降.. 哈哈
不会解释.. 但肯定答案应该是0.7071 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 12:54 PM
|
显示全部楼层
发表于 24-9-2004 12:54 PM
|
显示全部楼层
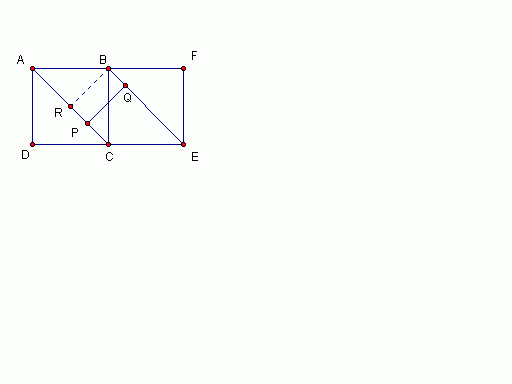
把立方体打开来看。
PQ 最短的距离是当PQ 直角的时候。
PQ = RB
ABCD = 正方形
RB = AR
AR = 1/2 AC
= 1.4142
PQ = 1.4142/2
= 0.7071 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 01:14 PM
|
显示全部楼层
发表于 24-9-2004 01:14 PM
|
显示全部楼层
fritlizt 于 24-9-2004 12:54 说 :

把立方体打开来看。
PQ 最短的距离是当PQ 直角的时候。
PQ = RB
ABCD = 正方形
RB = AR
AR = 1/2 AC
= 1.4142
PQ = 1.4142/2
...
啊... 对hor...
AC = 1.4142 啦.
PQ = AR |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|