|
查看: 6772|回复: 117
|
数学训练(十月份)
[复制链接]
|
|
|
基于之前的"数学训练~每日一题"里头的贴子算是蛮多的了,有网友向我反映在找答案是有点困难、有点眼花撩乱!!所以在这个十月份,开个新贴!!暂且命名为"数学训练(十月份)"。
十月份之后,我将"数学训练~每日一题"及"数学训练(十月份)"合并!!
另外,请有兴趣的网友留意:
我将所有的问题放在这个贴(第一面),每日更新题目!!这是为了避免问题四处 飞   
还是老样子:
我会每天都会贴一个数学题目(一般的比赛题目)。程度方面就由初中至高中,乃至大专都会有。
( 星期一至星期三:初中 (A)
星期四至星期三:高中 (B)
星期日 :大专 (C) )
我的用意是想让大家参与。所以程度浅的也有,深的也有,任君选择属于自己能力范围里的。也希望大家能多多互相讨论!!
请多多支持!!  
(答案最快在隔天公布)
(对于提高不提高积分,我觉得若是有兴趣"玩"的网友都不在意!!所以,玩得开心就好!!)
01/10/2004,星期五
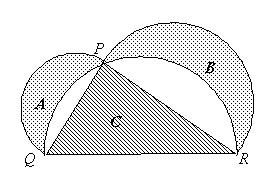
高中(B20) 如图,PQ,QR,RP 个别是个别圆的直径;而 A,B,C 则各为阴影部分的面积。
求证: A + B = C
 (已解) (已解)
(答案:--)
(解对者:fritlizt,eeCyang,sinchee,灰羊,38女)
02/10/2004,星期六
高中(B21) x 是任意实数,求证: cos(cos x) ≥ sin x 。 (已解)
(答案:--)
(解对者:sMIL3)
03/10/2004,星期日
大专(C7)
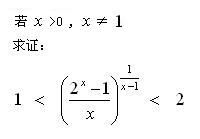
( 提示:利用 Mean Value Theorem ) (待解)
(答案:)
(解对者:)
04/10/2004,星期一
初中(A22) 当 1956, 1980 及 2004 除一正整数 a ,其余数均为 b 。
求 a + b 的最大值。 (已解)
(答案:36)
(解对者:38女)
05/10/2004,星期二
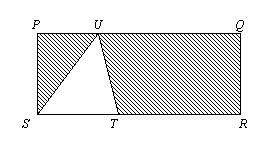
初中(A23) 如图, PQRS 为一长方形。已知 PQ = 3 PS,ST:SR = 1:3 。
求 三角形 SUT 的面积 和 阴影部分面积 之比。
 (已解) (已解)
(答案:1 : 5)
(解对者:史奴比{^_^})
06/10/2004,星期三
初中(A24) 已知 a = x + 1
b = x + 2
c = x + 3
求 a^2 + b^2 + c^2 - ab -bc - ca 之值。 (已解)
(答案:3)
(解对者:38女史奴比{^_^},止战之殇,灰羊,sMIL3)
07/10/2004,星期四
高中(B22)
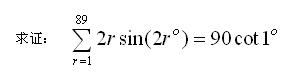 (已解) (已解)
(答案:--)
(解对者:sinchee)
08/10/2004,星期五
高中(B23) 有两堆棋子,数目相等.两人玩耍,每人可以在一堆里任意取几颗,但不能同时在两堆里取,规定取得最后一颗者胜。
求证后取者可以必胜。 (已解)
(答案:--)
(解对者:灰羊)
09/10/2004,星期六
高中(B24) 不许用计算机,试比较 e^π 与 π^e,哪个比较大? (已解)
(答案:e^π)
(解对者:sMIL3)
10/10/2004,星期日
大专(C8)
 (已解) (已解)
(答案:--)
(解对者:情~風)
11/10/2004,星期一
初中(A25) 若 a/b = b/c = c/d = d/a ,其中 abcd ≠0。
求 (a+b+c+d)/(a+b+c-d) 之值。 (已解)
(答案:0 或 2)
(解对者:史奴比{^_^},430201)
12/10/2004,星期二
初中(A26) 已知 A,B,C,D,E 为整数,且 0 ≤A,B,C,D,E≤9 。
若 A B C D E
x 4
_________________
E D C B A
----------
求 A,B,C,D,E 之值。 (已解)
(答案:(A,B,C,D,E)=(2,1,9,7,8))
(解对者:史奴比{^_^},灰羊,38女)
13/10/2004,星期三
初中(A27) 甲、乙兩人轮流报数,必须报不大於2的自然数,把兩人报的数加起來,
谁报数后加起來的数是20,谁就获胜。
如甲要取胜,是先报还是后报?报几?(请解释你的论点!) (已解)
(答案:甲先报。报 2)
(解对者:灰羊,fritlizt,38女)
14/10/2004,星期四
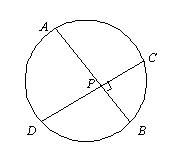
高中(B25) 如图,在圆 O 任意画二 互相垂直的(chord):AB 及 CD。
若 AB 与 CD 交点为 P 。
求证: AP^2 + PB^2 + CP^2 + PD^2 恒为某定值。
 (已解) (已解)
(答案:--)
(解对者:430201,灰羊)
15/10/2004,星期五
高中(B26) 若 a^3 + b^3 = 2.
求证 a + b ≤ 2. (已解)
(答案:--)
(解对者:430201)
16/10/2004,星期六
高中(B27) 已知 α 、β 为锐角,
且 3(sin α)^2 + 2(sin β)^2 = 1;
3(sin 2α) - 2(sin 2β) = 0,
求证: α + 2β = π/2 。 (已解)
(答案:--)
(解对者:灰羊)
17/10/2004,星期日
大专(C9) 求证:
 (已解) (已解)
(答案:--)
(解对者:灰羊,多普勒效应)
18/10/2004,星期一
初中(A28) 100 个学生排成一列,由左到右,报数!
1,2,3,...,100。
现在喊奇数的学生退出;喊偶数的学生保留,然后由左到右,报数!
1,2,3,...,50。
现在喊奇数的学生退出;喊偶数的学生保留,然后由左到右,报数!
1,2,3,...,25。
。。。
如此指令重复,直到最后一个学生!
问:这最后一个学生第一次喊什么号码? (已解)
(答案:64)
(解对者:430201,史奴比{^_^})
19/10/2004,星期二
初中(A29) 若 1/a + 1/b + 1/c = 1/(a+b+c),
求证 a^3 + b^3 + c^3 = (a+b+c)^3。 (已解)
(答案:--)
(解对者:多普勒效应,430201)
20/10/2004,星期三
初中(A30) 小明将 1,2,3,4,5,6,7,8,9 分别写在3X3的表格内(如下图),每格一个数字。
他分别将各(横)行,和各(竖)列的三个数加起来。
把和写在表的下方和右方。
试找出 * 之值。
 (已解) (已解)
(答案:7)
(解对者:多普勒效应,430201,史奴比{^_^})
21/10/2004,星期四
高中(B28) 我们设
指令(1)为:由左到右,报数! 喊奇数的学生退出;喊偶数的学生保留,
指令(2)为:由右到左,报数! 喊奇数的学生退出;喊偶数的学生保留,
100 个学生排成一列。
指令(1)
指令(2)
指令(1)
指令(2)
...
如此指令重复,直到最后一个学生!
问:这最后一个学生第一次喊什么号码? (已解)
(答案:54)
(解对者:430201)
22/10/2004,星期五
高中(B29) 若 0< a,b < 1 。
试求
√{a^2 + b^2} + √{(1-a)^2 + b^2} + √{(1-a)^2 + (1-b)^2} + √{a^2 + (1-b)^2}
的极小值。 (已解)
(答案:2√2)
(解对者:多普勒效应)
23/10/2004,星期六
高中(B30) 在三角形 ABC,角 C 为直角。
试求 (a+b)/c 的极大值及极小值。 (已解)
(答案:极大值=√2,没有 极小值...)
(解对者:多普勒效应)
24/10/2004,星期日
大专(C10) 若 0 < x ,y < 1 。
求证 1 < x^y + y^x < 2 。 (待解)
(答案:)
(解对者:)
25/10/2004,星期一
初中(A31) 若 (a+b)/(a-b) = 7/4
求 (a^2)/(b^2) 之值。 (已解)
(答案:121/9)
(解对者:多普勒效应,430201)
26/10/2004,星期二
初中(A32) 已知 六位数 174xyz 能被 7,11,13 整除。
求 x + y + z 。 (已解)
(答案:12)
(解对者:430201,史奴比{^_^})
27/10/2004,星期三
初中(A33) 在某一数,x 的前后各添上"1"。
得到的数 y, 比 x 大 13439。
求 x 。 (已解)
(答案:382)
(解对者:多普勒效应,430201,史奴比{^_^})
28/10/2004,星期四
高中(B31) 已知 a, b 为正整数,且 (a,b) 满足 10 < a^2 + b^2 < 28 。
问共有几组不同的 (a,b) ?
(答案:11) (已解)
(解对者:430201)
29/10/2004,星期五
高中(B32) (B32) 若 f(x) = (x-1)(x-2)(x-3)(x-4)…(x-10),
求 f '(10)。 (已解)
(答案:9!)
(解对者:ah_mok)
30/10/2004,星期六
高中(B33) 已知 x, y 为正整数,且 (x,y) 满足 1/x + 1/y = 1/30 。
求 y 的极大值。 (已解)
(答案:930)
(解对者:430201)
31/10/2004,星期日
大专(C11)
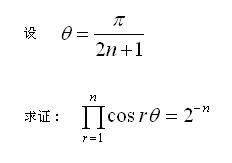 (待解) (待解)
(答案:)
(解对者:)
(不管是 已解 或 待解 的题目,欢迎网友们多多支持!让大家分享你们的 idea  谢谢 谢谢 
若各位网友有哪些有趣、适合的问题,请短消息给我!!)
[ Last edited by 多普勒效应 on 31-10-2004 at 09:30 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-9-2004 10:30 PM
|
显示全部楼层
发表于 30-9-2004 10:30 PM
|
显示全部楼层
pipi 于 30-9-2004 07:33 PM 说 :
基于之前的"数学训练~每日一题"里头的贴子算是蛮多的了,有网友向我反映在找答案是有点困难、有点眼花撩乱!!所以在这个十月份,开个新贴!!暂且命名为"数学训练 ...
QPR 是一个半圆。
所以角QPR = 90.
半圆PQ 的面积为 : pai * PQ^2 /8
半圆PR 的面积为 : pai * PR^2 /8
半圆RQ 的面积为 : pai * RQ^2 /8
有根据 phytagoras theorem, 半圆PQ 的面积 + 半圆PR 的面积 = 半圆RQ 的面积
再扣除白色的面积,
A+B = C
不好意思, 把8 type 成4。
[ Last edited by fritlizt on 1-10-2004 at 06:27 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 01:36 PM
|
显示全部楼层
发表于 1-10-2004 01:36 PM
|
显示全部楼层
我用的方法比较复杂...
因为我不懂phytagoras theorem...
首先我找 个别的半圆加起来的面积)-(整个图的面积)=白色的面积 个别的半圆加起来的面积)-(整个图的面积)=白色的面积
就如fritlizt所说:
QPR 是一个半圆。
所以角QPR = 90.
半圆PQ 的面积为 : pai * (PQ/2)^2/2
半圆PR 的面积为 : pai * (PR/2)^2/2
半圆RQ 的面积为 : pai * (RQ/2)^2/2
结果得:[pai * (PQ/2)^2/2 + pai * (PR/2)^2/2 + pai * (RQ/2)^2/2]
-[pai * (PQ/2)^2/2 + pai * (PR/2)^2/2 + PQ*PR/2]
得 pai * (RQ/2)^2/2 -PQ*PR/2 这是白色的面积...
过后我才用左式证:
A+B= pai* (PQ/2)^2/2 + pai* (PR/2)^2/2 -[pai* (RQ/2)^2/2 -PQ*PR/2]
C= PQ*PR/2
那如果要令到A+B=C.. 那pai* (PQ/2)^2/2 + pai* (PR/2)^2/2= pai* (RQ/2)^2/2
这和phytagoras theorem很像...
但如果不知道有这theorem..我就不会证下去了.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 02:01 PM
|
显示全部楼层
发表于 1-10-2004 02:01 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 02:20 PM
|
显示全部楼层
发表于 1-10-2004 02:20 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 02:48 PM
|
显示全部楼层
发表于 1-10-2004 02:48 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 1-10-2004 06:18 PM
|
显示全部楼层
fritlizt 于 30-9-2004 10:30 PM 说 :
QPR 是一个半圆。
所以角QPR = 90.
半圆PQ 的面积为 : pai * PQ^2 /8
半圆PR 的面积为 : pai * PR^2 /8
半圆RQ 的面积为 : pai * RQ^2 /8
有根据 phytagoras theorem, 面积PQ + 面积PR = 面积RQ
再扣除白色的面积,
A+B = C
你的做法正确,不过
面积PQ + 面积PR = 面积RQ
写得不明确!!
什么是面积PQ呢??
eeCyang 于 1-10-2004 01:36 PM 说 :
我用的方法比较复杂...
因为我不懂phytagoras theorem...
phytagoras theorem...是你学过的"毕氏定理"!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 06:21 PM
|
显示全部楼层
发表于 1-10-2004 06:21 PM
|
显示全部楼层
pipi 于 1-10-2004 06:18 PM 说 :
你的做法正确,不过
面积PQ + 面积PR = 面积RQ
写得不明确!!
什么是面积PQ呢??
phytagoras theorem...是你学过的"毕氏定理"!!
阿哈, 刚才赶着去上课, 只是简简单单的解释一下。
现在又要出去了, 迟些回来再edit.
不好意思。
  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 08:29 PM
|
显示全部楼层
发表于 1-10-2004 08:29 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-10-2004 12:17 AM
|
显示全部楼层
发表于 2-10-2004 12:17 AM
|
显示全部楼层

<img src="http://home.pchome.com.tw/online/hycheah2000/cari1.GIF"> |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-10-2004 11:46 AM
|
显示全部楼层
发表于 2-10-2004 11:46 AM
|
显示全部楼层
02/10/2004,星期六
高中(B21)
x 是任意实数,求证: cos(cos x) ≥ sin x 。 (待解)
(答案:)
(解对者:)
-1<=cosx<=1,
cos(cosx)>0>=cos57'18 (cos1=cos57'18=cos-1)cos57'18=0.54024032...
当0<=x<=90', cos57'18<=cos(cosx)<=1, 0<=sinx<=1.
cos(cosx)和sinx的graf 相交与x=90'.
在0<=x<90',cos(cosx)>sinx
当90'<x<=180', 1<cos(cosx)<=cos57'18, 1<sinx<=0
同样的,cos(cosx)>sinx
在180'<x<=360'也得到cos(cosx)>sinx..
这样一直重复,所以cos(cos x) ≥ sin x , 当x 是任意实数..
但我觉得这样的解释还不够说服力,我会再努想其他方法...    |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-10-2004 12:40 AM
|
显示全部楼层
发表于 4-10-2004 12:40 AM
|
显示全部楼层
以我的程度只能證一半
當π≦x≦2π
sin x≦0
(sin在第三第四象限為負值)
cos(cos x)≧0
(因為在第三第四象限-1≦cos x≦1
∴cos(cos x)≧0)
故當π≦x≦2π時,
cos(cos x)≧sin x
恆成立 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-10-2004 05:04 PM
|
显示全部楼层
发表于 4-10-2004 05:04 PM
|
显示全部楼层
当 1956, 1980 及 2004 除一正整数 a ,其余数均为 b 。
求 a + b 的最大值。 (待解)
(答案:)
(解对者:)
我的数学不好,可以加入吗?
我是这么猜的:
1980 - 1956 = 24
2004 - 1956 = 48
gcd(24,48) = 24
因此,12 ≡ 1956 (mod 24)
≡ 1980 (mod 24)
≡ 2004 (mod 24)
a = 24;b = 12
a + b = 36 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 5-10-2004 10:08 AM
|
显示全部楼层
38女 于 4-10-2004 05:04 PM 说 :
我的数学不好,可以加入吗?
我是这么猜的:
我是这么猜的:
1980 - 1956 = 24
2004 - 1956 = 48
gcd(24,48) = 24
因此,12 ≡ 1956 (mod 24)
≡ 1980 (mod 24)
≡ 2004 (mod 24)
a = 24;b = 12
a + b = 36
38女,欢迎加入!!
你的答案是对的!!!
恭喜!!恭喜!!
有空常来!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-10-2004 11:56 AM
|
显示全部楼层
发表于 5-10-2004 11:56 AM
|
显示全部楼层
|
好可怜,我已是大专生,但只懂得解初中题目……我还在努力尝试大专题目,高中那题,我解了,但答案似乎和别人一样,所以就没发上来了。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-10-2004 01:24 PM
|
显示全部楼层
发表于 5-10-2004 01:24 PM
|
显示全部楼层
05/09/2004,星期二
初中(A23) 如图, PQRS 为一长方形。已知 PQ = 3 PS,ST:SR = 1:3 。
求 三角形 SUT 的面积 和 阴影部分面积 之比。
若把PS=1, PQ = 3
那么,PQRS 面积 = 3
ST : SR = PS : PQ (SR=PQ, ST=PS)
= 1 : 3
SUT 面积 = 1/2 (ST*PS)
= 1/2
阴部分面积 = PQRS 面积 - SUT 面积
= 3 - 1/2
= 5/2
那么,SUT 面积 : 阴部分面积 = (1/2) : (5/2)
= 1 : 5
对吗? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 5-10-2004 02:02 PM
|
显示全部楼层
eeCyang 于 2-10-2004 11:46 AM 说 :
-1<=cosx<=1,
cos(cosx)>0>=cos57'18 (cos1=cos57'18=cos-1)cos57'18=0.54024032...
当0<=x<=90', cos57'18<=cos(cosx)<=1, 0<=sinx<=1.
cos(cosx)和sinx的graf 相交与x=90'.
在0<=x<90',cos(cosx)>sinx
当90'<x<=180', 1<cos(cosx)<=cos57'18, 1<sinx<=0
同样的,cos(cosx)>sinx
在180'<x<=360'也得到cos(cosx)>sinx..
这样一直重复,所以cos(cos x) ≥ sin x , 当x 是任意实数..
灰羊 于 4-10-2004 12:40 AM 说 :
以我的程度只能證一半
當π≦x≦2π
sin x≦0
(sin在第三第四象限為負值)
cos(cos x)≧0
(因為在第三第四象限-1≦cos x≦1
∴cos(cos x)≧0)
故當π≦x≦2π時,
cos(cos x)≧sin x
恆成立
这两种方法都是可行,只是没有将问题完全地解决!!
当0<=x<=90', cos57'18<=cos(cosx)<=1, 0<=sinx<=1.
cos(cosx)和sinx的graf 相交与x=90'.
在0<=x<90',cos(cosx)>sinx
(不过。。。这该如何证明??)
或者各位可参考 微中子 之前在回答 多普勒效应
"sin cos X =cos sin X"
的解法!!
38女 于 5-10-2004 11:56 AM 说 :
好可怜,我已是大专生,但只懂得解初中题目……
我们的教育制度没有教会我们思考吧! 
塞进去脑袋的充其量是一大堆的公式!!  
也许你的答案有那么一点点跟别人不一样,贴上来吧。。。也许其他人能够从你的观点得到启发,也不一定!!
[ Last edited by pipi on 22-10-2004 at 10:35 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-10-2004 08:42 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-10-2004 09:47 AM
|
显示全部楼层
发表于 6-10-2004 09:47 AM
|
显示全部楼层
06/10/2004,星期三
初中(A24) 已知 a = x + 1
b = x + 2
c = x + 3
求 a^2 + b^2 + c^2 - ab -bc - ca 之值。 (待解)
(答案:)
(解对者:)
解:
b = a + 1; c = a + 2
a^2 + b^2 + c^2 - ab -bc - ca
= a^2 + (a + 1)^2 + (a + 2)^2 - a(a + 1) - (a + 1)(a + 2) - (a + 2)a
= a^2 + a^2 + 2a + 1 + a^2 + 4a + 4 - a^2 - a - a^2 -3a - 2 - a^2 - 2a
= 1 + 4 - 2
= 3 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-10-2004 10:07 AM
|
显示全部楼层
发表于 6-10-2004 10:07 AM
|
显示全部楼层
06/10/2004,星期三
初中(A24) 已知 a = x + 1
b = x + 2
c = x + 3
求 a^2 + b^2 + c^2 - ab -bc - ca 之值。
另一个方法:
(a-b)^2 = a^2 + b^2 - 2ab
(b-c)^2 = b^2 + c^2 - 2bc
(c-a)^2 = c^2 + a^2 - 2ca
(a-b)^2 + (b-c)^2 + (c-a)^2 = 2a^2 + 2b^2 + 2c^2 - 2ab - 2bc - 2ca
除以2 :
[(a-b)^2 + (b-c)^2 + (c-a)^2]/2 = a^2 + b^2 + c^2 - ab - bc - ca (如题目所要的)
a-b = -1, b-c = -1 , c-a = 2
答案: a^2 + b^2 + c^2 - ab - bc - ca = [(-1)^2 + (-1)^2 + (2)^2]/2
= 6/2
= 3 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|