|
查看: 11301|回复: 235
|
数学训练~每日一题
[复制链接]
|
|
|
正如我在"逻辑数学论坛意见箱、讨论区(大家请进^^)"
http://chinese.cari.com.my/myfor ... 5wnN&sid=465wnN
里提出的,这个礼拜起,我会每天都会贴一个数学题目(一般的比赛题目)。程度方面就由初中至高中,乃至大专都会有。
( 大概是这样:
星期一至星期三:初中 (A)
星期四至星期三:高中 (B)
星期日 :大专 (C) )
我的用意是想让大家参与。所以程度浅的也有,深的也有,任君选择属于自己能力范围里的。也希望大家能多多互相讨论!!
请多多支持!!  
(答案最快在隔天公布)
答对三题者的积分将被提高,以示鼓励!!  
16/08/2004,星期一
初中(A1) 不可用计算机,找出下列的值:
(16082004)(26082004) - (16082005)(26082003) (已解)
(答案:-9999999)
(解对者:無聊人,强,chwk87)
17/08/2004,星期二
初中(A2) 若 x^2 + 2x + 3 = 0 。
求 x^4 + 4x^3 + 7x^2 + 6x + 3 之值。 (已解)
(答案:3)
(解对者:無聊人,chwk87,辉文)
18/08/2004,星期三
初中(A3) 若 n 为自然数,求证 n^3 + 3(n^2)/2 + n/2 能被 3 整除。 (已解)
(答案:--)
(解对者:fritlizt,强)
19/08/2004,星期四
高中(B1) 已知 (y+z)/(b+c) = (z+x)/(c+a) = (x+y)/(a+b),
求证 (x+2y-3z)/(4x+5y-6z) = (a+2b-3c)/(4a+5b-6c) (已解)
(答案:--)
(解对者:辉文,sinchee)
20/08/2004,星期五
高中(B2) a,b,c,d 为任意正数,设 S = a/(a+b+d) + b/(a+b+c) + c/(b+c+d) + d/(a+c+d)
求证: 1 < S < 2 (已解)
(答案:--)
(解对者:sinchee)
21/08/2004,星期六
高中(B3) 已知 7^82 + 8^161 能被 57 整除,
求证 7^83 + 8^163 也能被 57 整除。 (已解)
(答案:--)
(解对者:fritlizt,强,飞彦)
22/08/2004,星期日
大专(C1) 设 p(x) = a + bx + 3cx^2 + dx^3 + 5ex^4 为一实数多项式。
已知 a + c + e = 0,求证 p(x) = 0 在区间 [-1,1] 中有一实根。 (已解)
(答案:--)
(解对者:**)
23/08/2004,星期一
初中(A4) 不可用计算机(或对数表(sifir)),决定以下的最大值(并说出原因):
(a) 6^100 (b) 5^200 (c) 4^300 (d) 3^400 (e) 2^500 (已解)
(答案:(d) 3^400)
(解对者:fritlizt)
24/08/2004,星期二
初中(A5) 某年的六月份里有三个星期三是奇数,该月的13日是星期几? (已解)
(答案:星 期 一 )
(解对者:chwk87,快乐)
25/08/2004,星期三
初中(A6) 若 x/(a-b) = y/(b-c) = z/(c-a),求 x + y + z 。 (已解)
(答案:0)
(解对者:chwk87,快乐)
26/08/2004,星期四
高中(B4) 求证
(i) 数列 11,111,1111,...
(ii) 数列 44,444,4444,...
中的每一项都不是完全平方数。 (已解)
(答案:--)
(解对者:sinchee)
27/08/2004,星期五
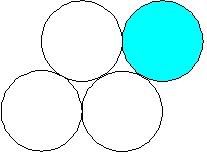
高中(B5) 如图,四个一角钱硬币,其中蓝色的沿着其他三个滚了一圈,直到回到原位为止。
请问蓝色的硬币,共转了多少度? (已解)
(答案:1080度)
(解对者:微中子,sinchee)
28/08/2004,星期六
高中(B6) 设 n (>3) 为自然数且 n, n+2 为质数。
求证 n+1 是 6 的倍数。 (已解)
(答案:--)
(解对者:sinchee)
29/08/2004,星期日
大专(C2) 设 f(x) 为可微(differentiable)偶函数 (即 f(-x) = f(x) for all x)。求证
(i) f '(x) 为奇函数 (即 f '(-x) = - f '(x) for all x)。
(ii) f '(0) = 0 (已解)
(答案:--)
(解对者:sinchee)
29/08/2004,星期日
大专(C2)' a,b,c 为整数。
若 a^2 + b^2 + c^2 是 16 的倍数,
求证 a^3 + b^3 + c^3 是 64 的倍数。 (已解)
(答案:--)
(解对者:辉文,微中子)
30/08/2004,星期一
初中(A7) 设 a 为 x^2 + x + 1 = 0 的其中一个解。
求 1/(1-a) + 1/(1- a^2) 。 (已解)
(答案:1)
(解对者:sinchee)
31/08/2004,星期二
初中(A8) 不可用计算机,找出下列的值:
99999 * 77778 + 33333 * 66666 。 (已解)
(答案:9999900000)
(解对者:sooshi,止战之殇)
1/09/2004,星期三
初中(A9) 若 x < 0, x - 1/x = 1 。 求 x + 1/x 之值。 (已解)
(答案:- sqrt(5))
(解对者:sinchee)
2/09/2004,星期四
高中(B7) 若 (1)(1!)+(2)(2!)+(3)(3!)+...+(1001)(1001!) 除以 2004,求其余数。 (已解)
(答案:2003)
(解对者:sinchee)
3/09/2004,星期五
高中(B8) 设 0< a < 90(度),sin(a) + cos(a) = sqrt(2)。
求 sin(a) + sin(2a) + ... + sin(8a) 之值。 (已解)
(答案:0)
(解对者:陈敏慧)
4/09/2004,星期六
高中(B9) 若 (a+b)/(a-b) = (b+c)/(2(b-c)) = (c+a)/(3(c-a)),
求证: 8a + 9b + 5c = 0 (已解)
(答案:--)
(解对者:陈敏慧,sinchee)
5/09/2004,星期日
大专(C3) k 为正整数, 求证:
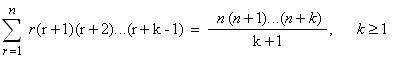 (已解) (已解)
(答案:--)
(解对者:微中子)
6/09/2004,星期一
初中(A10) 在 3 点与 4 点之间,时钟的长针和短针重合的时间是多少? (已解)
(答案:3点16分21.8秒)
(解对者:jolin~yo~yo,强,sinchee)
7/09/2004,星期二
初中(A11) 试证:三个连续奇数的平方和 加上 1,不能被 24 整除。 (已解)
(答案:--)
(解对者:chwk87,flyingfish)
8/09/2004,星期三
初中(A12) 把 10^4 - 4 计算出来的号码(即 10000 - 4 = 9996)的每个数字(即 9,9,9,6)加起来,可得 9+9+9+6=33。
那么把 10^809 - 809 计算出来的号码的每个数字加起来又是多少呢? (已解)
(答案:7265)
(解对者:ANNIE^_^LIM)
9/09/2004,星期四
高中(B10) 若 n 为自然数,求证 n^2 + n + 2 不能被 15 整除。 (已解)
(答案:--)
(解对者:sinchee)
10/09/2004,星期五
高中(B11) 若 n 为整数,
试将 1 + 1/n^2 + 1/(n+1)^2 可写成 (a/b)^2 的形式,其中 a,b 为整数。 (已解)
(答案:[(n(n+1)+1)/n(n+1)]^2)
(解对者:chwk87,强)
11/09/2004,星期六
高中(B12) 把1600粒花生分给100只猴子。
证明:不管怎样分,至少有4只猴子得到的花生一样多。
能否找到一种分法,使得没有5只猴子得到同样多的花生。 (已解)
(答案:--)
(解对者:sinchee)
12/09/2004,星期日
大专(C4) 在边长为 2 的正六边形上任意点 25 个点。
证明:存在着两点,其距离小于 1。 (已解)
(答案:--)
(解对者:sinchee)
13/09/2004,星期一
初中(A13) 若 abc = 1, 求证: 1/(ab+a+1) + 1/(bc+b+1) + 1/(ac+c+1) = 1 (已解)
(答案:--)
(解对者:止战之殇,430201)
14/09/2004,星期二
初中(A14) 某场戏剧的入门票为成人 RM30,学生 RM15。
这戏剧是在拥有 600 张座位的礼堂举行。
当局共卖出价值 RM15000 的入门票。
已知仍有一些座位空置,那么学生的人数最多为___。 (已解)
(答案:198)
(解对者:sinchee )
15/09/2004,星期三
初中(A15) OX 及 OY 是圆 O 的半径。
XMY 是以 XY 为直径的半圆。
如图所示, T,S,C 分别为各个部分的面积。
那么 T 之比为___。 之比为___。
 (已解) (已解)
(答案:1:1)
(解对者:chwk87)
16/09/2004,星期四
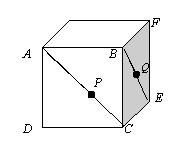
高中(B13) 下图所示为边长为 1 的正方体。
AC 及 BE 为对角线。P、Q 分别是 AC 及 BE 上的点。
那么 PQ (沿着立方体表面)的最短距离为___。
 (已解) (已解)
(答案:1/√2)
(解对者:fritlizt)
17/09/2004,星期五
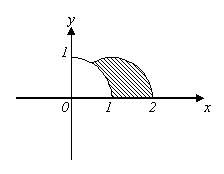
高中(B14) 图中所示为两个半径为 1 的圆,其中心分别为原点及(1,0)。
求阴影部分的面积(答案以 π 或根号(surd form)来表示)。
 (已解) (已解)
(答案:1/6 π + √3/4)
(解对者:sinchee)
18/09/2004,星期六
高中(B15) 证明:
 (已解) (已解)
(答案:--)
(解对者:sinchee)
19/09/2004,星期日
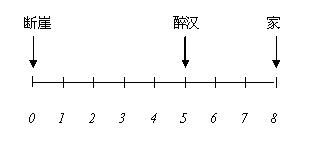
大专(C5) 某个醉汉目前在位置 "5",他的家在位置 "8",而位置 "0" 则是断崖。
由于他分不清方向,设他每次移动一单位,且只走向左或向右,而每次向左或向右的机率皆为 1/2。
若到位置 "8",则家人迎接他(安全抵达)。
若到位置 "0", 则跌入断崖。。。(无法继续行程)
求此醉汉安全回到家的机率。
 (已解) (已解)
(答案:5/8)
(解对者:sinchee,斷羽鳥)
20/09/2004,星期一
初中(A16) 不可用计算机,求 x:
x / 1200905200904 = 1160804 / 1200904 (已解)
(答案:1160805160804)
(解对者:止战之殇)
21/09/2004,星期二
初中(A17) A 是含有 21 数字的偶数。
已知 A 是完全平方数,及 A 的十位数为 6。
那么 A 的个位数则为__。 (已解)
(答案:4)
(解对者:sinchee)
22/09/2004,星期三
初中(A18) 若实数 a,b 满足 0 < a < b 和 a^2 + b^2 = 6ab,
那么(a+b)/(a-b) 为 _______。 (已解)
(答案:-√2)
(解对者:止战之殇,430201)
23/09/2004,星期四
高中(B16) 若 a,b 为 方程式 x^2 + 6x + 1 = 0 之根,
求 (√a + √b)^2 之值。 (已解)
(答案:- 8)
(解对者:fritlizt)
24/09/2004,星期五
高中(B17) 设 {a} 为任意的等差数列,其公差为 d,而且{a}的每一项皆是整数。
若 w,x,y,z 为{a} 连续的四项。
证明:wxyz + d^4 是个完全平方数。 (已解)
(答案:--)
(解对者:止战之殇)
25/09/2004,星期六
高中(B18)
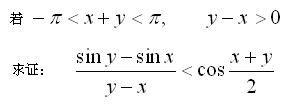 (已解) (已解)
(答案:--)
(解对者:sinchee)
26/09/2004,星期日
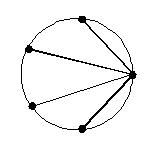
大专(C6) 如下图,在单位圆(即半径为 1)的圆周上取 5 个点。
(将这5点连起来,可形成正五边形)
现在,5 点中任选 1 点,将此点接连其余 4 点,得四个线段.
设这四个线段的长度分别为 a,b,c,d。
求证: abcd = 5
 (已解) (已解)
(答案:--)
(解对者:止战之殇,fritlizt)
27/09/2004,星期一
初中(A19) 不可用计算机,找出下列的值:
√{5 + √(21)} + √{5 - √(21)}
(答案以根号(surd form)来表示) (已解)
(答案:√14)
(解对者:eeCyang)
28/09/2004,星期二
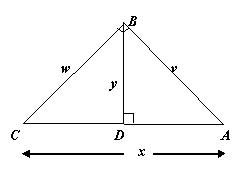
初中(A20) 如图,角 ABC 及 角 BDA 皆是直角。
若 v + w = 35,x + y = 37,
求 y 之值。
 (已解) (已解)
(答案:12)
(解对者:eeCyang)
29/09/2004,星期三
初中(A21) 若 x < -2,试简化 |1-|1+x||。 (已解)
(答案:-2-x)
(解对者:eeCyang)
30/09/2004,星期四
高中(B19)
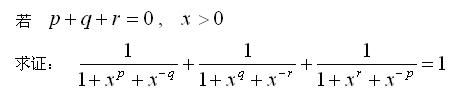 (已解) (已解)
(答案:--)
(解对者:eeCyang,止战之殇)
敬请留意:
(明天)下个月起,"数学训练"将开个新贴!!
标题也是类似"数学训练(十月份)"。
(不管是 已解 或 待解 的题目,欢迎网友们多多支持!让大家分享你们的 idea  谢谢 谢谢 
若各位网友有哪些有趣、适合的问题,请短消息给我!!)
[ Last edited by pipi on 21-10-2004 at 11:50 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 11:18 AM
|
显示全部楼层
发表于 16-8-2004 11:18 AM
|
显示全部楼层
pipi网友,我想题目应该是
(16082004)(16082004) - (16082005)(16082003)
吧? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-8-2004 11:57 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 03:32 PM
|
显示全部楼层
发表于 16-8-2004 03:32 PM
|
显示全部楼层
flash 于 16-8-2004 11:18 AM 说 :
pipi网友,我想题目应该是
(16082004)(16082004) - (16082005)(16082003)
吧?
大家不妨可以先做这题先。。。  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 05:08 PM
|
显示全部楼层
发表于 16-8-2004 05:08 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 05:31 PM
|
显示全部楼层
发表于 16-8-2004 05:31 PM
|
显示全部楼层
题目是 (16082004)(16082004) - (16082005)(16082003) 或 (16082004)(26082004) - (16082005)(26082003) ?????
如果是(16082004)(16082004) - (16082005)(16082003) 的话。那答案等于1
a^2-(a+1)(a-1) = a^2-(a^2-1) = a^2-a^2+1 = 1
[ Last edited by fritlizt on 16-8-2004 at 05:38 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-8-2004 05:42 PM
|
显示全部楼层
fritlizt 于 16-8-2004 05:31 PM 说 :
1
a^2-(a+1)(a-1) = a^2-(a^2-1) = a^2-a^2+1 = 1
你是做哪一题呢??
(16082004)(16082004) - (16082005)(16082003)
或
(16082004)(26082004) - (16082005)(26082003)
我的题目是(16082004)(26082004) - (16082005)(26082003)
不过玩玩(16082004)(16082004) - (16082005)(16082003) 也无妨。
我相信这两题对你来说都不是问题。。。
無聊人 于 16-8-2004 05:08 PM 说 :
是-9999999吗?
对!!!
其他初中的朋友,请试试吧!!
[ Last edited by pipi on 16-8-2004 at 06:06 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 05:44 PM
|
显示全部楼层
发表于 16-8-2004 05:44 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-8-2004 05:55 PM
|
显示全部楼层
DarknessAngel 于 16-8-2004 05:44 PM 说 :
答案是'1'吧.....
的算法是 ( 4 * 4 ) - ( 5 * 3 ) = 1
因为前面的都一样,所以就可以免了吧。。
不知道对不对。。。。。
试算算:
(44)(54) - (43)(55) 及 (44)(54)-(45)(53)
会不会是 1 呢??
[ Last edited by pipi on 16-8-2004 at 06:05 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 06:54 PM
|
显示全部楼层
发表于 16-8-2004 06:54 PM
|
显示全部楼层
|
ab-(a+1)(b-1)=ab-(ab+b-a-1)=a-b+1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-8-2004 08:36 PM
|
显示全部楼层
发表于 16-8-2004 08:36 PM
|
显示全部楼层
(16082004)(26082004) - (16082005)(26082003)
=(16082004)(26082003+1) - (16082004+1)(26082003)
=(16082004)(26082003)+(16082004) - (16082004)(26082003)-(26082003)
=16082004-26082003
=-9999999 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-8-2004 02:41 PM
|
显示全部楼层
发表于 17-8-2004 02:41 PM
|
显示全部楼层
若 x^2 + 2x + 3 = 0 。
求 x^4 + 4x^3 + 7x^2 + 6x + 3 之值。
这题相信大家都会吧。。。
  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-8-2004 04:25 PM
|
显示全部楼层
发表于 17-8-2004 04:25 PM
|
显示全部楼层
强 于 17-8-2004 02:41 PM 说 :
若 x^2 + 2x + 3 = 0 。
求 x^4 + 4x^3 + 7x^2 + 6x + 3 之值。
这题相信大家都会吧。。。
 
Is it 3? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-8-2004 08:52 PM
|
显示全部楼层
发表于 17-8-2004 08:52 PM
|
显示全部楼层
X^2+2X+3=0
So, x^2+2x=-3
(x^2+2x)=(-3)^2
x^4+4x^3+4X^2=9
x^4+4x^3+4X^2+3x^2+6x+3=9+3x^2+6x+3
x^4+4x^3+7X^2+6x+3=3(X^2+2X+3+1)
=3(0+1)
=3
[ Last edited by chwk87 on 17-8-2004 at 09:02 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-8-2004 10:10 AM
|
显示全部楼层
发表于 18-8-2004 10:10 AM
|
显示全部楼层
若 n 为自然数,求证 n^3 + 3(n^2)/2 + n/2 能被 3 整除。
n=4??? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-8-2004 11:42 AM
|
显示全部楼层
发表于 18-8-2004 11:42 AM
|
显示全部楼层
强 于 17-8-2004 14:41 说 :
若 x^2 + 2x + 3 = 0 。
求 x^4 + 4x^3 + 7x^2 + 6x + 3 之值。
这题相信大家都会吧。。。
 
无聊人、chwk87,答案是对的。
x^4 + 4x^3 + 7x^2 + 6x + 3
=x^4 + 2x^3 + 3x^2 + 2x^3 + 4x^2 + 6x + 3
=x^2(x^2 + 2x + 3) + 2x ( x^2 + 2x + 3) +3
=3 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 18-8-2004 05:56 PM
|
显示全部楼层
若 n 为自然数,求证 n^3 + 3(n^2)/2 + n/2 能被 3 整除。
各位网友,不要吝啬给出解答,请"慷慨解囊"!!
强 于 18-8-2004 10:10 AM 说 :
n=4???
强,n 为自然数。。。(我有回答到你的问题吗?) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-8-2004 10:37 PM
|
显示全部楼层
发表于 18-8-2004 10:37 PM
|
显示全部楼层
18/08/2004,星期三
初中(A3) 若 n 为自然数,求证 n^3 + 3(n^2)/2 + n/2 能被 3 整除。 (待解)
(答案:n=18)
n^3 + 3(n^2)/2 + n/2 = n^3(2) + 3(n^2)/2 (2) + n/2 (2)
= 2n^3 + 3(n^2) + n
= 2n^3 + 3n^2 + n (如n是1)
= 2^3 + 3^2 +1
= 8 + 9 + 1
= 18
能被 3 整除 = 18/3 = 6
[ Last edited by Leong_hikaru on 20-8-2004 at 11:30 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-8-2004 10:48 PM
|
显示全部楼层
发表于 18-8-2004 10:48 PM
|
显示全部楼层
初中(A3) 若 n 为自然数,求证 n^3 + 3(n^2)/2 + n/2 能被 3 整除。
n^3 + 3(n^2)/2 + n/2 = (2n^3+3(n^2)+n)/2
2n^3+3(n^2)+n 肯定是偶数。 所以只要考虑 2n^3+3(n^2)+n 即可。3(n^2)肯定能被三整除。
只要证 2n^3+n 能被三除即可。
2n^3+n = n(2n^2+1)
有三个condition.
1.n=3k
2.n=3k+1
3.n=3k+2
当n等于3k时。
n(2n^2+1) = 3k(2(3k)^2+1)
能被三除。
当n等于3k+1时。
n(2n^2+1) = (3k+1)(2(3k+1)^2+1)
= (3k+1)(18k^2+12k+2+1)
= 3(3k+1)(6k^2+4k+1)
能被三除 。
当n等于3k+2时。
n(2n^2+1) = (3k+2)(2(3k+2)^2+1)
= (3k+2)(18k^2+24k + 9)
= 3(3k+2)(6k^2+8k+3)
能被三除
所以n^3 + 3(n^2)/2 + n/2
能被三除。
给任何n
对吗???
有没有比较简单的方法???
[ Last edited by fritlizt on 18-8-2004 at 10:51 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-8-2004 11:29 PM
|
显示全部楼层
发表于 18-8-2004 11:29 PM
|
显示全部楼层
Leong_hikaru 于 18-8-2004 22:37 说 :
18/08/2004,星期三
初中(A3) 若 n 为自然数,求证 n^3 + 3(n^2)/2 + n/2 能被 3 整除。 (待解)
(答案:n=9)
题目好象要求证明而已,不是找出n的值。注意"求证"这个字
用数学归纳法也可以证明
由于n是自然数,因此n=0是无效的。从n=1开始吧!
设n=1,式子n^3 + 3(n^2)/2 + n/2 =1+3/2+1/2
= 3
因此命题成立。
另外设n=k,命题也成立,即式子K^3 + 3(k^2)/2+k/2能被3整除。
当n=k+1时, (k+1)^3+ 3(k+1)/2+ (K+1)/2
=(k+1)/2[ 2(+1)^2 +(k+1)+1]
=(k+1)/2[(2k+3)(k+2)]
这就是说当n=k+1时,命题也成立。
[ Last edited by 辉文 on 18-8-2004 at 11:41 PM ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|